Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ème partie - Exercice 1
20 min
35
La fonction est définie sur par .
Question 1
Déterminer l'ensemble de dérivabilité de la fonction .
Correction
est une fonction polynôme du ème degré.
Par définition, les fonctions polynomiales sont dérivables sur .
Il en résulte donc, que la fonction est dérivable sur .
Par définition, les fonctions polynomiales sont dérivables sur .
Il en résulte donc, que la fonction est dérivable sur .
Question 2
Calculer la dérivée de sur son domaine de dérivabilité.
Correction
est dérivable sur .
Question 3
Déterminer une équation de la tangente à la courbe au point d'abscisse .
Correction
L'équation de la tangente au point d'abscisse s'écrit .
Ici , ce qui donne, .Avec et .
1ère étape : calculer
2ème étape : calculer
3ème étape : on remplace les valeurs de et de dans la formule de l'équation de tangente.
On sait que :
Ainsi l'équation de la tangente à la courbe au point d'abscisse est alors .
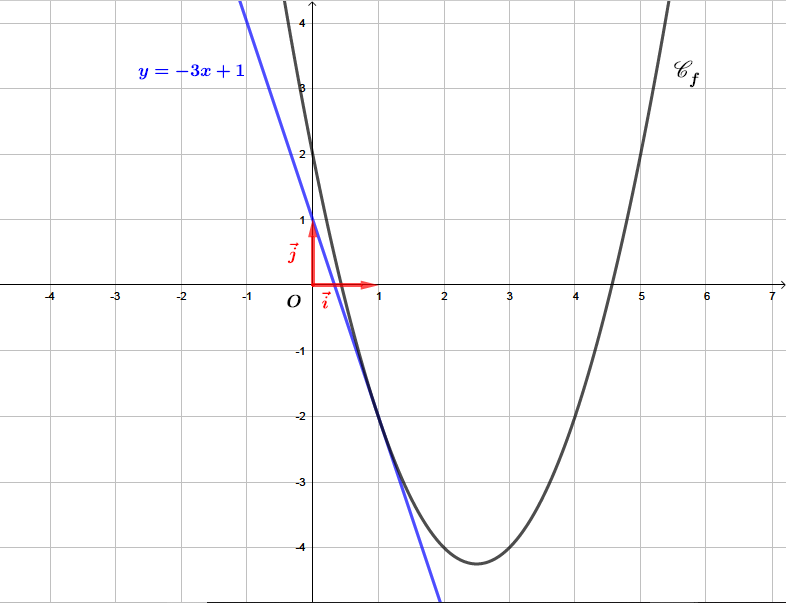
Question 4
Etudier le signe de
Correction
Etudier le signe de équivaut successivement à :
est un polynôme du second degrzé de la forme
1ère étape : On définit les valeurs , et .
Ainsi :
Donc
3ème étape : Calcul des racines suivant le signe du discriminant .
Comme alors l'équation admet une racine double réelle notée telle que :
ainsi d'où
4ème étape : Le tableau de signe du trinôme du second degré qui dépend du signe du discriminant .
Comme et que nous connaissons la racine , le tableau de signe du trinôme du second degré va dépendre du signe de . Ici
.

est un polynôme du second degrzé de la forme
1ère étape : On définit les valeurs , et .
- nombre devant d'où
- nombre devant d'où
- nombre seul d'où
Ainsi :
Donc
3ème étape : Calcul des racines suivant le signe du discriminant .
Comme alors l'équation admet une racine double réelle notée telle que :
ainsi d'où
4ème étape : Le tableau de signe du trinôme du second degré qui dépend du signe du discriminant .
Comme et que nous connaissons la racine , le tableau de signe du trinôme du second degré va dépendre du signe de . Ici
.

Question 5
En déduire la position relative de la courbe de par rapport à la droite .
Correction
La position relative entre deux courbes étudie les intervalles sur lesquelles une des courbes est supérieure à l'autre.
Pour étudier la position relative entre et , il faut étudier le signe de .
De la question précédente, on en a déduit que : Pour étudier la position relative entre et , il faut étudier le signe de .
- Si sur un intervalle alors la courbe représentative de est au-dessus de sur .
- Si sur un intervalle alors la courbe représentative de est en dessous de sur .
- Si en un point de l'intervalle alors la courbe représentative de et ont un point en commun en .
.


Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.