Exercices types : $$1$$^ère partie - Exercice 1

D'après la lecture graphique, on a :

• $$f(1)=-8$$
• $$f(2)=-9$$
• $$f(3)=-8$$

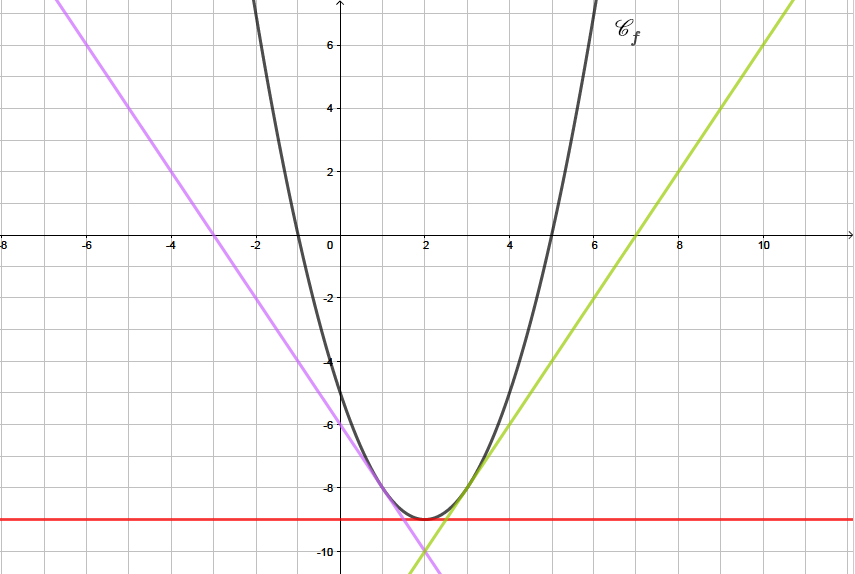
$$f'\left(1\right)$$ correspond au coefficient directeur de la tangente à la courbe au point d'abscisse $$1$$. Il s'agit ici de la droite violette.

Les points $$A\left(1;-8\right)$$ et $$B\left(0;-6\right)$$ appartiennent à cette tangente.
A l'aide du point $$A$$ et du point $$B$$ on va pouvoir donner le coefficient directeur de la tangente.
$$f'\left(1\right)=\frac{y_{B} -y_{A} }{x_{B} -x_{A} }$$
$$f'\left(1\right)=\frac{-6-\left(-8\right)}{0-1}$$
Ainsi :

$$f'\left(2\right)$$ correspond au coefficient directeur de la tangente à la courbe au point d'abscisse $$2$$. Il s'agit ici de la droite rouge.

La tangente est horizontale. Cela signifie que le coefficient directeur est nul.
Ainsi :

$$f'\left(3\right)$$ correspond au coefficient directeur de la tangente à la courbe au point d'abscisse $$3$$. Il s'agit ici de la droite verte.

Les points $$A\left(3;-8\right)$$ et $$B\left(4;-6\right)$$ appartiennent à cette tangente.
A l'aide du point $$A$$ et du point $$B$$ on va pouvoir donner le coefficient directeur de la tangente.
$$f'\left(3\right)=\frac{y_{B} -y_{A} }{x_{B} -x_{A} }$$
$$f'\left(3\right)=\frac{-6-\left(-8\right)}{4-3}$$
Ainsi :