Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient fin janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : Problèmes Optimisation - Exercice 2
20 min
35
Une entreprise vend des logiciels (licences spécialisées) mathématiques pour les lycées. Le bénéfice réalisé par cette vente de logiciels, en une semaine, est modélisée par la fonction . Le bénéfice est exprimé en euros.
L'entreprise ne peut pas fournir plus de logiciels par semaine, on aura ainsi : .
L'entreprise ne peut pas fournir plus de logiciels par semaine, on aura ainsi : .
Question 1
Calculer le bénéfice pour licences.
Correction
Il nous faut calculer .
L'entreprise réalisera un bénéfice de euros pour une vente de licences.
L'entreprise réalisera un bénéfice de euros pour une vente de licences.
Question 2
Calculer la dérivée de .
Correction
Soit ; est dérivable sur .
Il vient :
Il vient :
Question 3
Etudier les variations de .
Correction
Nous savons que pour tout réel , on a : .
Ici la dérivée est une fonction du ème degré.
Pour l'étude du signe de , on va utiliser le discriminant.
Alors ; et .
Or donc .
Il existe donc deux racines réelles distinctes.
On en déduit le tableau de variation suivant :
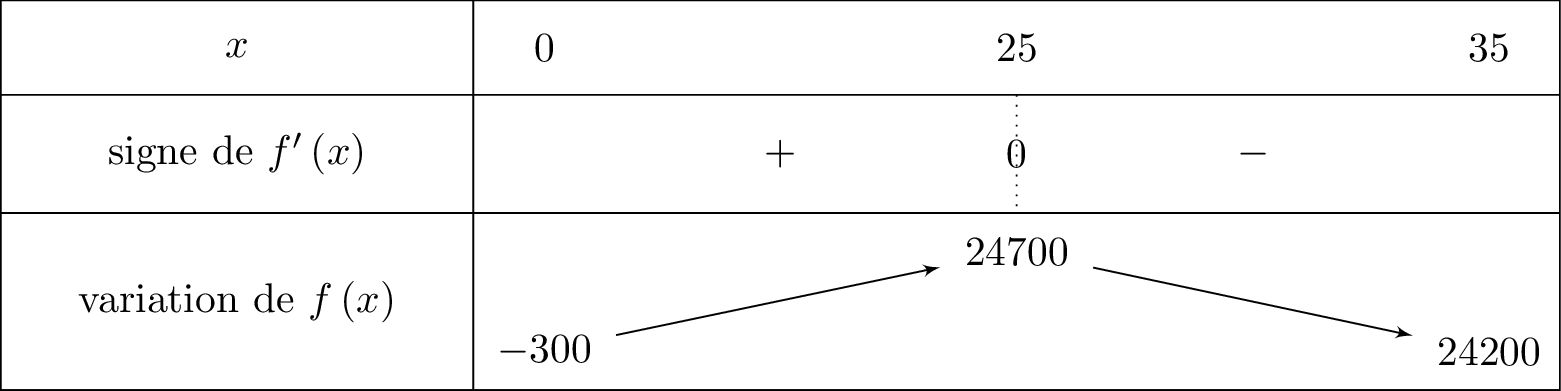 De plus :
De plus :
Ici la dérivée est une fonction du ème degré.
Pour l'étude du signe de , on va utiliser le discriminant.
Alors ; et .
Or donc .
Il existe donc deux racines réelles distinctes.
- ce qui donne .
- ce qui donne .
On en déduit le tableau de variation suivant :

Question 4
En déduire combien de licences l’entreprise doit fabriquer et vendre par semaine pour avoir un bénéfice maximal.
Correction
D'après le tableau de variation précédent, on indique en rouge le maximum et sa valeur.
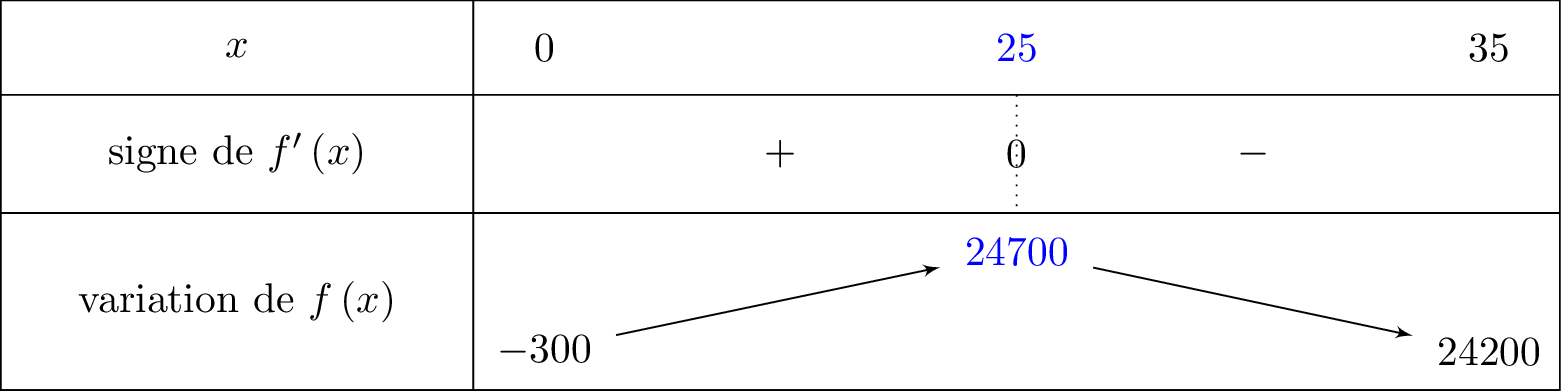 Ainsi l’entreprise doit fabriquer et vendre chaque semaine licences pour avoir un bénéfice maximal dont le montant sera de euros.
Ainsi l’entreprise doit fabriquer et vendre chaque semaine licences pour avoir un bénéfice maximal dont le montant sera de euros.

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.