Exercices types : $$4$$^ème partie - Exercice 1

Pour répondre à la question, nous allons dresser le tableau de variation complet de la fonction $$f$$.
$$f$$ est dérivable sur $$\mathbb{R}$$. Il vient alors que :
$$f'\left(x\right)=-\frac{2}{3} \times 3x^{2} -2x+4$$
$$f'\left(x\right)=-2x^{2} -2x+4$$
Ici la dérivée est une fonction du $$2$$^ème degré.
Pour l'étude du signe de $$-2x^{2} -2x+4$$, on va utiliser le discriminant.
Alors $$a=-2$$; $$b=-2$$ et $$c=4$$.
Or $$\Delta =b^{2} -4ac$$ donc $$\Delta =\left(-2\right)^{2} -4\times \left(-2\right)\times 4=36$$.
Il existe donc deux racines réelles distinctes.

• $$x_{1} =\frac{-b-\sqrt{\Delta } }{2a}$$ ce qui donne $$x_{1} =1$$.
• $$x_{2} =\frac{-b+\sqrt{\Delta } }{2a}$$ ce qui donne $$x_{2} =-2$$.

Comme $$a=-2<0$$, la parabole est tournée vers le bas c'est-à-dire que $$f$$ est du signe de $$a$$ à l'extérieur des racines et du signe opposé à $$a$$ entre les racines.
On en déduit le tableau de variation suivant :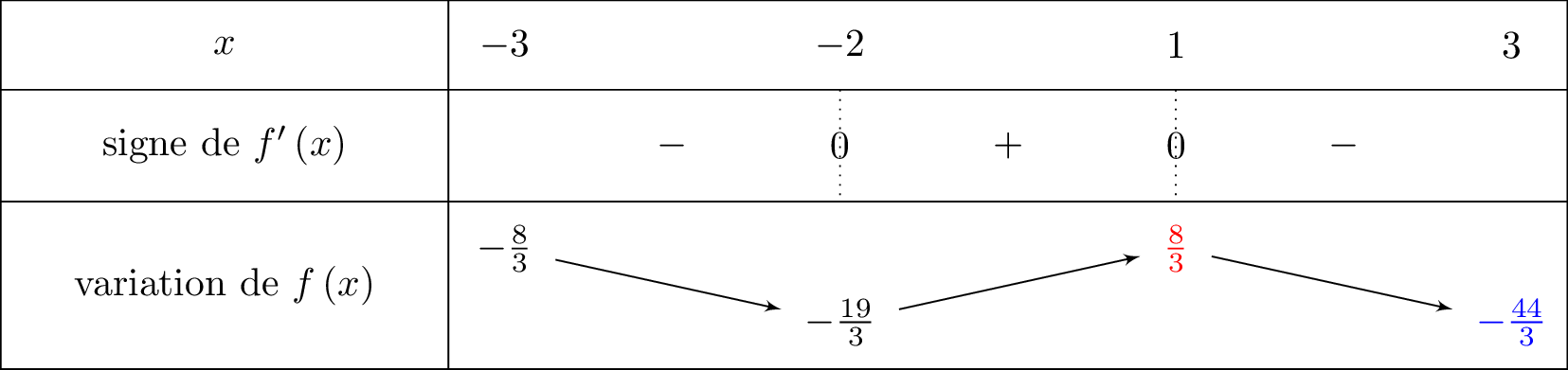Nous allons détailler les valeurs obtenues dans le tableau de variation :

$$f\left(-3\right)=-\frac{2}{3}\times \left(-3\right)^{3} -\left(-3\right)^{2} +4\times \left(-3\right)+\frac{1}{3}$$ ce qui donne $$f\left(-3\right)=-\frac{8}{3}$$

$$f\left(-2\right)=-\frac{2}{3}\times \left(-2\right)^{3} -\left(-2\right)^{2} +4\times \left(-2\right)+\frac{1}{3}$$ ce qui donne $$f\left(-2\right)=-\frac{19}{3}$$

$$f\left(1\right)=-\frac{2}{3}\times 1^{3} -1^{2} +4\times 1+\frac{1}{3}$$ ce qui donne $$f\left(1\right)=\frac{8}{3}$$

$$f\left(3\right)=-\frac{2}{3}\times 3^{3} -3^{2} +4\times 3+\frac{1}{3}$$ ce qui donne $$f\left(3\right)=-\frac{44}{3}$$

Pour trouver un encadrement de la fonction $$f$$ pour $$x\in \left[-3;3\right]$$ , nous allons nous aider du tableau de variation . Il nous faut déterminer le minimum et le maximum de $$f$$ .
Le minimum de $$f$$ vaut $${\color{blue}-\frac{44}{3}}$$ lorsque $$x=3$$ .
Le minimum de $$f$$ vaut $${\color{red}\frac{8}{3}}$$ lorsque $$x=1$$ .
Il en résulte donc que pour tout réel $$x\in \left[-3;3\right]$$ , on a :