Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : ème partie - Exercice 2
15 min
30
La fonction est définie sur par .
Question 1
Déterminer une équation de la tangente à la courbe au point d'abscisse .
Correction
L'équation de la tangente au point d'abscisse s'écrit .
Ici , ce qui donne, .1ère étape : calculer la dérivée de
alors :
2ème étape : calculer
3ème étape : calculer
4ème étape : on remplace les valeurs de et de dans la formule de l'équation de tangente.
On sait que :
Ainsi l'équation de la tangente à la courbe au point d'abscisse est alors
Question 2
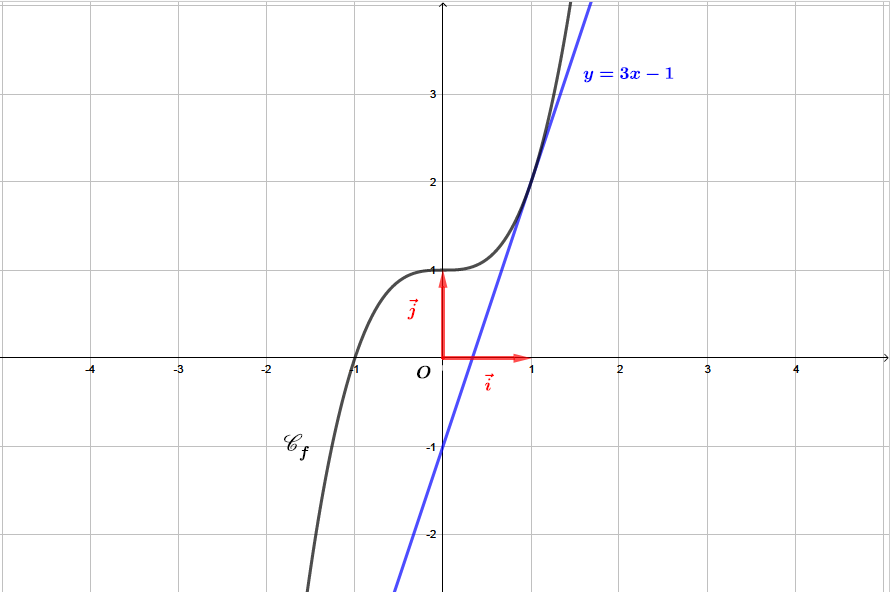
Existe-t-il une tangente à parallèle à la droite d'équation ? Justifier .
Correction
L'équation de la tangente au point d'abscisse s'écrit .
Nous savons donc, de manière générale, que l'équation de la tangente est de la forme . Si nous développons cette expression, on obtiendrait :. Le terme en bleu correspond donc au coefficient directeur de cette droite .
Or nous voulons que soit parallèle à la droite d'équation .
Or deux droites sont parallèles si les coefficients directeurs sont égaux. Il en résulte donc que :
. Comme est une abscisse que l'on recherche, nous allons prendre à la place de comme inconnue pour faciliter nos calculs. (enfin c'est pour revenir à des équations classiques avec des ).
Nous voulons donc résoudre l'équation :
. Comme . Alors :
équivaut successivement à :
Or un carré est toujours positif ou nul.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.