Applications de la dérivation
Comment étudier les variations d'une fonction de la forme - Exercice 3
15 min
25
Question 1
Soit la fonction définie sur par .
Déterminer l'expression de la dérivée de . Etudier le signe de en fonction de . En déduire le tableau de variation de . Cela peut également se résumer en une question : étudier les variations de sur .
Correction
- Si est négative sur alors est décroissante sur .
- Si est positive sur alors est croissante sur .
Ici la dérivée est une fonction du ème degré.
Pour l'étude du signe de , on va utiliser le discriminant.
Alors ; et .
Or donc .
Il existe donc deux racines réelles distinctes.
- ce qui donne d'où : .
- ce qui donne d'où : .
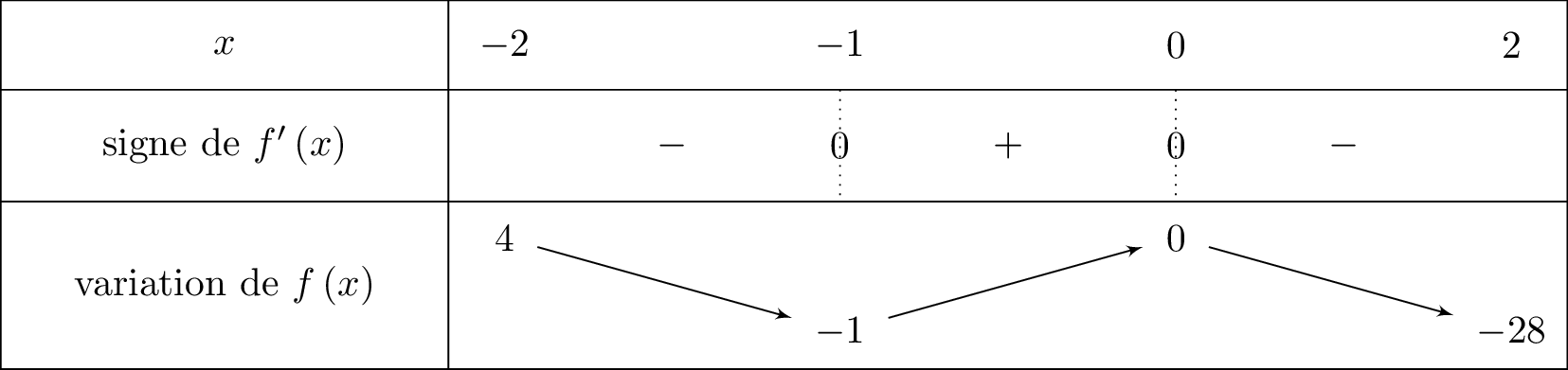
On en déduit le tableau de variation suivant :
Question 2
Soit la fonction définie sur par .
Déterminer l'expression de la dérivée de . Etudier le signe de en fonction de . En déduire le tableau de variation de . Cela peut également se résumer en une question : étudier les variations de sur .
Correction
- Si est négative sur alors est décroissante sur .
- Si est positive sur alors est croissante sur .
Ici la dérivée est une fonction du ème degré.
Pour l'étude du signe de , on va utiliser le discriminant.
Alors ; et .
Or donc .
Il existe donc deux racines réelles distinctes.
- ce qui donne d'où : .
- ce qui donne d'où : .
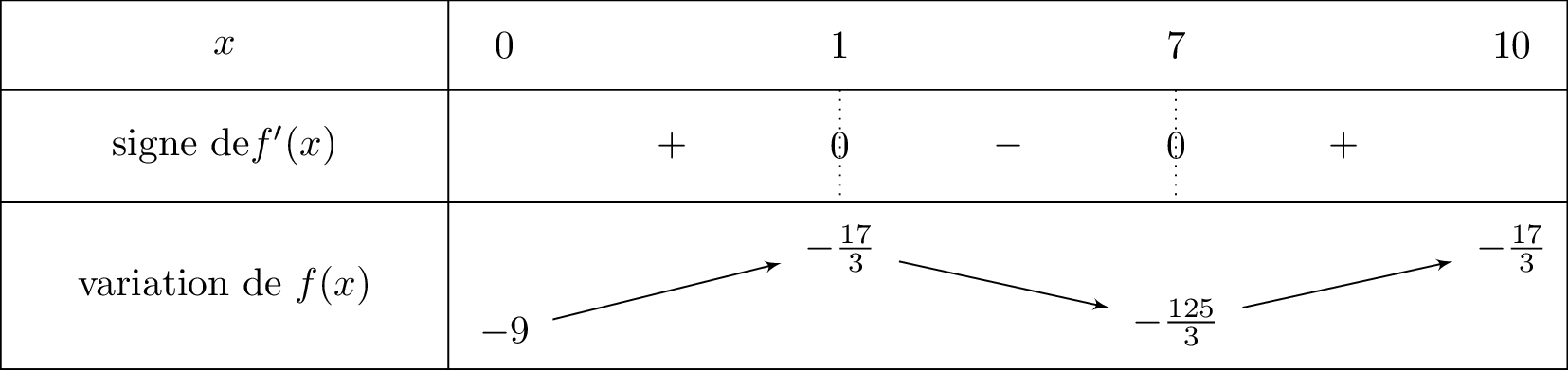
On en déduit le tableau de variation suivant :