Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
À l'aide de la calculatrice, déterminer une équation de la droite d'ajustement de en par la méthode des moindres carrés - Exercice 2
15 min
30
Un adepte de la bourse s'intéresse de près à la valorisation d'une entreprise depuis presque maintenant ans. Il a noté, année par année, l'évolution tarifaire de l'action présentée ci-dessous :

Question 1
Représenter dans un repère orthogonal le nuage de points de coordonnées associées à cette série statistique.
Correction
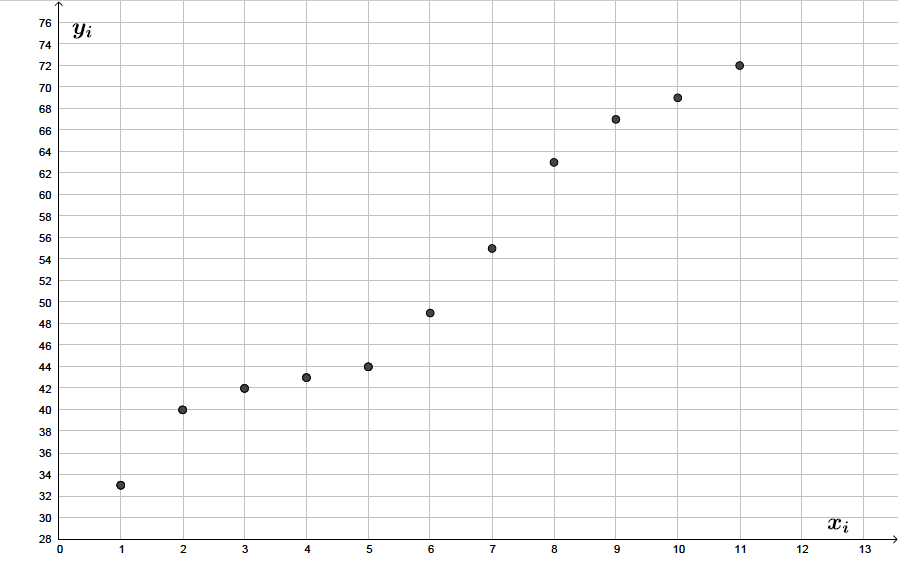
Question 2
Calculer les coordonnées du point moyen . Placer ensuite, sur le graphique précédent, le point .
Correction
Le point moyen d'un nuage de points est le point dont l'abscisse est la moyenne des abscisses , et l'ordonnée la moyenne des ordonnées .
Ses coordonnées vérifient donc : et .
Les coordonnées du point moyen de cette série statistique sont :Ses coordonnées vérifient donc : et .
Les coordonnées du point moyen sont :
Nous allons donc maintenant placer le point moyen dans le repère :
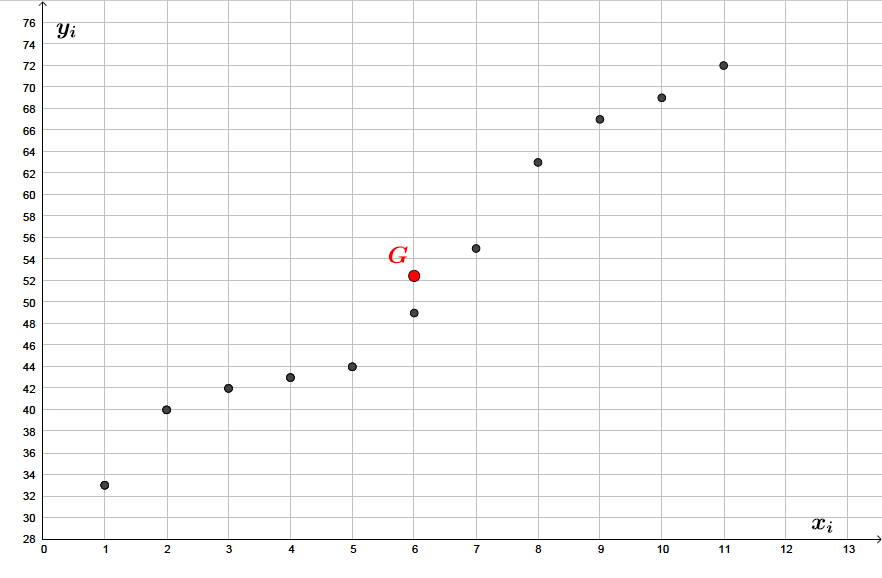
Question 3
À l'aide de la calculatrice, déterminer une équation de la droite d'ajustement de en , obtenue par la méthode des moindres carrés. Les coefficients seront arrondis à près.
Correction
Une équation de la droite d'ajustement de en par la méthode des moindres carrés obtenue à l'aide de la calculatrice, est (coefficients arrondis à près)
Question 4
Tracer la droite dans le même repère que le nuage de points.
Correction
Par exemple pour , nous avons . Notons ce deuxième point.
La droite passe par et par le point .
Nous traçons maintenant la droite dans le repère.
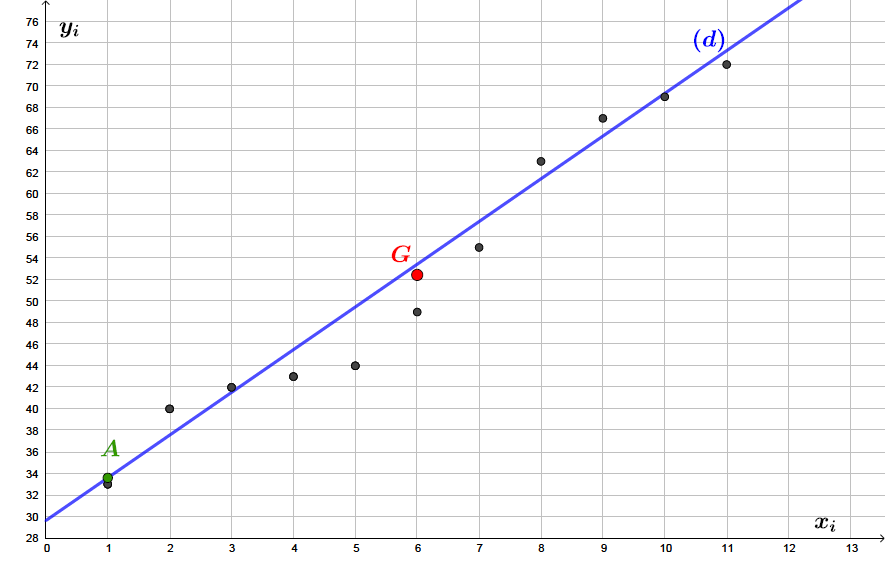
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.