Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Probabilités conditionnelles

Sous formes de problèmes - Exercice 2

16 min
30
Un conservatoire de musique propose deux parcours à ses élèves : un parcours diplômant et un parcours loisir. On observe que 40%40\% des élèves choisissent le parcours diplômant. Parmi ceux qui ont sélectionné le parcours diplômant, 30%30\% choisissent de faire partie d’un orchestre. Parmi les élèves ayant choisi le parcours loisir, 25%25\% choisissent de faire partie d’un orchestre. On sélectionne un élève de ce conservatoire au hasard.
On considère les évènements suivants :
  • DD : " L’élève sélectionné a choisi le parcours diplômant ".
  • LL : " L’élève sélectionné a choisi le parcours loisir ".
  • OO : " L’élève sélectionné a choisi de faire partie d’un orchestre ".
Question 1

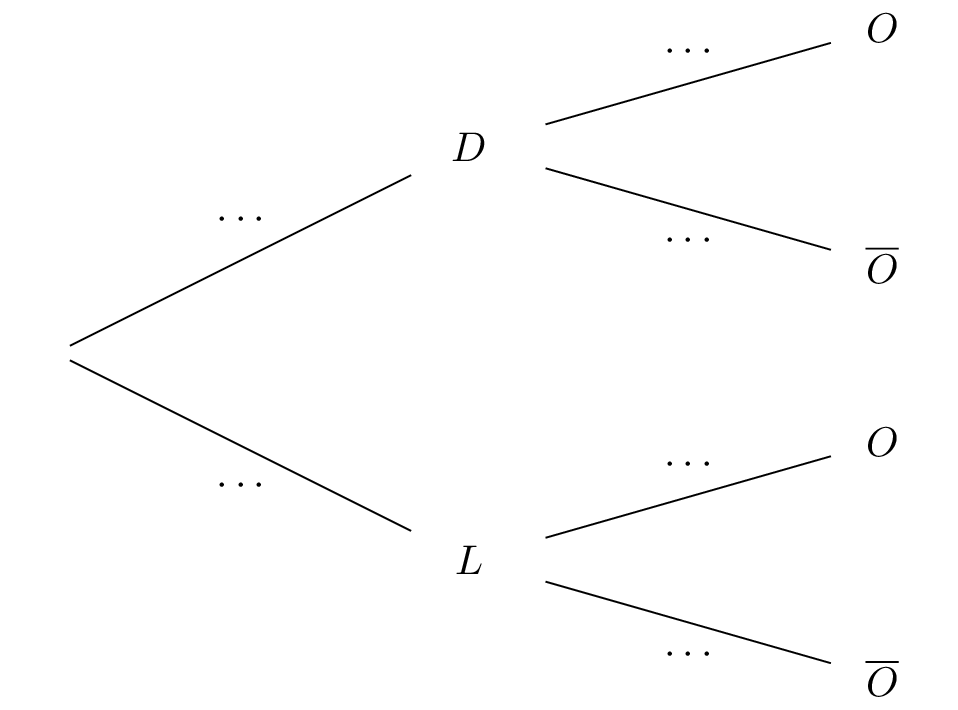
Compléter l’arbre de probabilité ci-dessus.

Correction
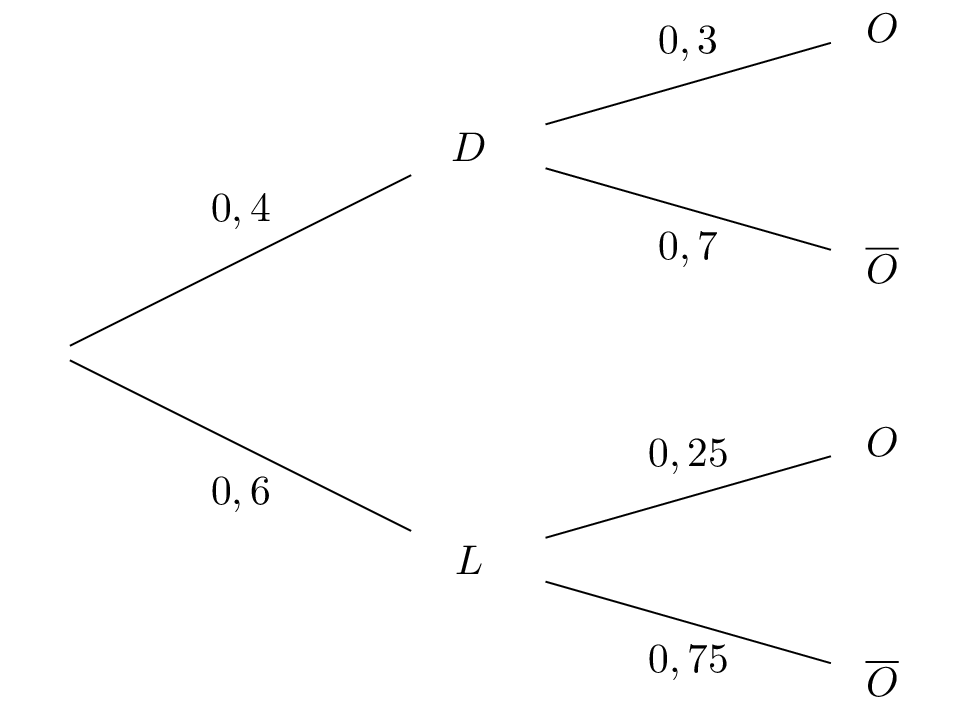
Question 2

Décrire par une phrase l’événement D∩OD\cap O puis calculer sa probabilité.

Correction
L'évènement D∩OD\cap O correspond à l'évènement : l’élève sélectionné a choisi le parcours diplômant et{\color{blue}{\text{et}}} de faire partie d’un orchestre .
P(D∩O)=P(D)×PD(O)P\left(D\cap O\right)=P\left(D\right)\times P_{D} \left(O\right)
P(D∩O)=0,4×0,3P\left(D\cap O\right)=0,4\times 0,3
P(D∩O)=0,12P\left(D\cap O\right)=0,12
Question 3

Déterminer la probabilité de l’évènement OO.

Correction
DD et LL forment une partition de l'univers.
D'après la formule des probabilités totales on a :
P(O)=P(D∩O)+P(L∩O)P\left(O\right)=P\left(D\cap O\right)+P\left(L\cap O\right)
P(O)=P(D)×PD(O)+P(L)×PL(O)P\left(O\right)=P\left(D\right)\times P_{D} \left(O\right)+P\left(L\right)\times P_{L} \left(O\right)
Soit : P(O)=0,4×0,3+0,6×0,25P\left(O\right)=0,4\times 0,3 +0,6\times 0,25
Ainsi :
P(O)=0,27P\left(O\right)=0,27

Question 4

On choisit au hasard un élève faisant partie d’un orchestre. Quelle est la probabilité, arrondie au millième, qu’il suive un parcours diplômant?

Correction
Il s'agit ici d'une forme avec un "sachant" c'est-à-dire une probabilité conditionnelle.
On pourrait traduire la question de la manière suivante ; sachant{\color{blue}{\text{sachant}}} que l'élève fait partie d'un orchestre, quelle est la probabilité qu'il suive un parcourt diplômant.
  • PB(A)=P(A∩B)P(B)P_{B} \left(A\right)=\frac{P\left(A\cap B\right)}{P\left(B\right)}

Il vient alors que :
PO(D)=P(D∩O)P(O)P_{O} \left(D\right)=\frac{P\left(D\cap O\right)}{P\left(O\right)}
PO(D)=P(D)×PD(O)P(O)P_{O} \left(D\right)=\frac{P\left(D\right)\times P_{D} \left(O\right)}{P\left(O\right)}
PO(D)=0,4×0,30,27P_{O} \left(D\right)=\frac{0,4\times 0,3}{0,27} d'où :
PO(D)≈0,444P_{O} \left(D\right)\approx 0,444