Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →

Exercices types : 1^ère partie - Exercice 3

25 min

Une enquête a été réalisée auprès des élèves d’un lycée afin de connaître leur sensibilité au développement durable et leur pratique du tri sélectif. L’enquête révèle que

70

% des élèves sont sensibles au développement durable, et, parmi ceux qui sont sensibles au développement durable,

80

% pratiquent le tri sélectif. Parmi ceux qui ne sont pas sensibles au développement durable, on en trouve

10

% qui pratiquent le tri sélectif.

Question 1

On interroge un élève au hasard dans le lycée. On considère les évènements suivants :

S

: L’élève interrogé est sensible au développement durable.

T

: L’élève interrogé pratique le tri sélectif.

Les résultats seront arrondis à

10^{-2}

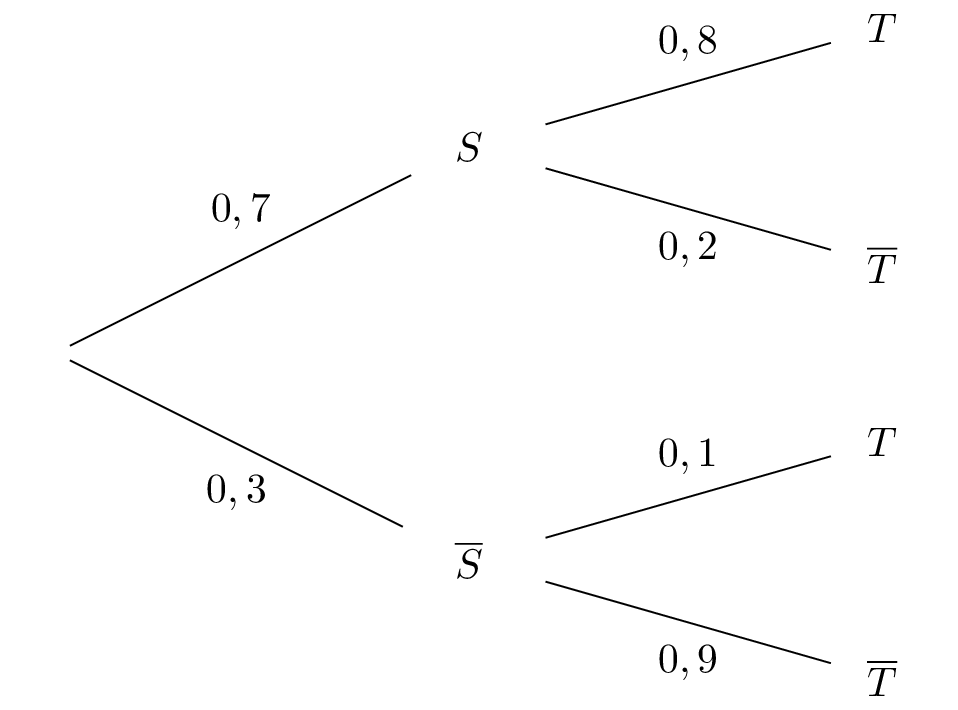
Construire un arbre pondéré décrivant la situation.

Correction

D'après l'énoncé on obtient l'arbre suivant:

Question 2

Calculer la probabilité que l’élève interrogé soit sensible au développement durable et pratique le tri sélectif.

Correction

L’évènement «l’élève interrogé est sensible au développement durable

{\color{blue}{\text{et}}}

pratique le tri sélectif» se traduit par :

S\cap T

.
Il en résulte que :

P\left(S\cap T\right)=P\left(A\right)\times P_{S} \left(T\right)

P\left(S\cap T\right)=0,7\times 0,8

P\left(S\cap T\right)=0,56

Question 3

Montrer que la probabilité $P\left(T\right)$ de l’évènement $T$ est $0,59$ .

Correction

Les évènements

S

\overline{S}

forment une partition de l'univers.
D'après la formule des probabilités totales, on a :

P\left(T\right)=P\left(S \cap T\right)+P\left(\overline{S} \cap T\right)

équivaut successivement à :

P\left(T\right)=P\left(S\right)\times P_{S} \left(T\right)+P\left(\overline{S}\right)\times P_{\overline{S}} \left(T\right)

P\left(T\right)=0,7\times 0,8 + 0,3\times 0,1

P\left(T\right)=0,59

Question 4

On interroge un élève qui ne pratique pas le tri sélectif. Peut-on affirmer que les chances qu’il se dise sensible au développement durable sont inférieures à $10$ %?

Correction

Il s'agit ici de déterminer une probabilité conditionnelle. Il nous faut donc calculer

P_{\overline{T}} \left(S\right)

P_{\overline{T}} \left(S\right)=\frac{P\left(S\cap \overline{T}\right)}{P\left(\overline{T}\right)}

P_{\overline{T}} \left(S\right)=\frac{P\left(S\cap \overline{T}\right)}{1-P\left(T\right)}

P_{\overline{T}} \left(S\right)=\frac{0,7\times 0,2}{1-0,59}

P_{\overline{T}} \left(S\right)\approx0,34

Les chances qu’il se dise sensible au développement durable sont de

34

% donc on en pas affirmation est fausse.

Exercices types : 1ère partie - Exercice 3

Construire un arbre pondéré décrivant la situation.

Calculer la probabilité que l’élève interrogé soit sensible au développement durable et pratique le tri sélectif.

Montrer que la probabilité P(T)P\left(T\right)P(T) de l’évènement TTT est 0,590,590,59.

On interroge un élève qui ne pratique pas le tri sélectif. Peut-on affirmer que les chances qu’il se dise sensible au développement durable sont inférieures à 101010%?

Exercices types : 1^ère partie - Exercice 3

Montrer que la probabilité $P\left(T\right)$ de l’évènement $T$ est $0,59$ .

On interroge un élève qui ne pratique pas le tri sélectif. Peut-on affirmer que les chances qu’il se dise sensible au développement durable sont inférieures à $10$ %?