Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ème partie - Exercice 1
20 min
35
Une entreprise de livraison de colis à domicile demande à un cabinet comptable de réaliser une étude sur son activité. Une partie des données concerne les bénéfices (en milliers d’euros) réalisés chaque année depuis 2012. Ces informations sont résumées dans le tableau ci-dessous :


Question 1
Déterminer le taux d’évolution global du bénéfice entre et .
Arrondir le résultat à près.
Arrondir le résultat à près.
Correction
- Soit la valeur initiale d’une grandeur et sa valeur finale suite à une évolution.
- Le taux d’évolution de cette grandeur est égal à
- En pourcentage, le taux d’évolution se note avec
- Si , il s’agit d’une augmentation.
- Si , il s’agit d’une diminution.
- La valeur initiale vaut ici .
- La valeur finale vaut ici .
équivaut successivement à :
Le bénéfice entre et a connu une augmentation d'environ
Question 2
Représenter dans un repère orthogonal le nuage de points de coordonnées associées à cette série statistique.
Correction
On place successivement les points de coordonnées , , , , et 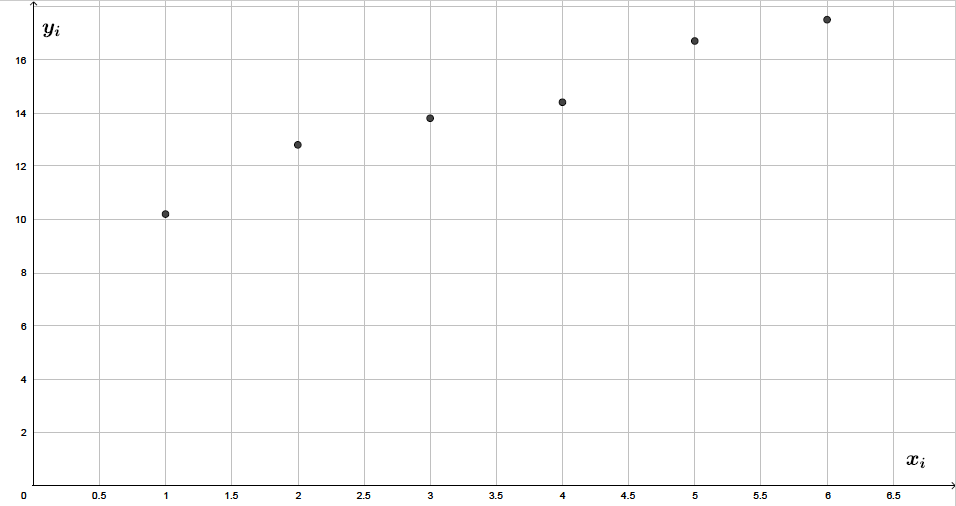

Question 3
À l’aide de la calculatrice, déterminer pour cette série statistique une équation de la droite d’ajustement de en obtenue par la méthode des moindres carrés. Arrondir les coefficients à près.
Correction
À la calculatrice, une équation de la droite d’ajustement de en obtenue par la méthode des moindres carrés est :
Question 4
Pour les deux questions suivantes, on prendra comme ajustement affine la droite d’équation .
Tracer cette droite sur le nuage de point .
Correction
Pour tracer la droite dans le nuage de point, il nous suffit de déterminer deux points appartenant à .
Nous choisissions, par exemple, puis .
Ainsi :
. Le premier point appartenant à la droite admet comme coordonnées .
. Le deuxième point appartenant à la droite admet comme coordonnées .
Il vous suffit de placer ces deux points et ensuite de tracer la droite comme donnée ci-dessous :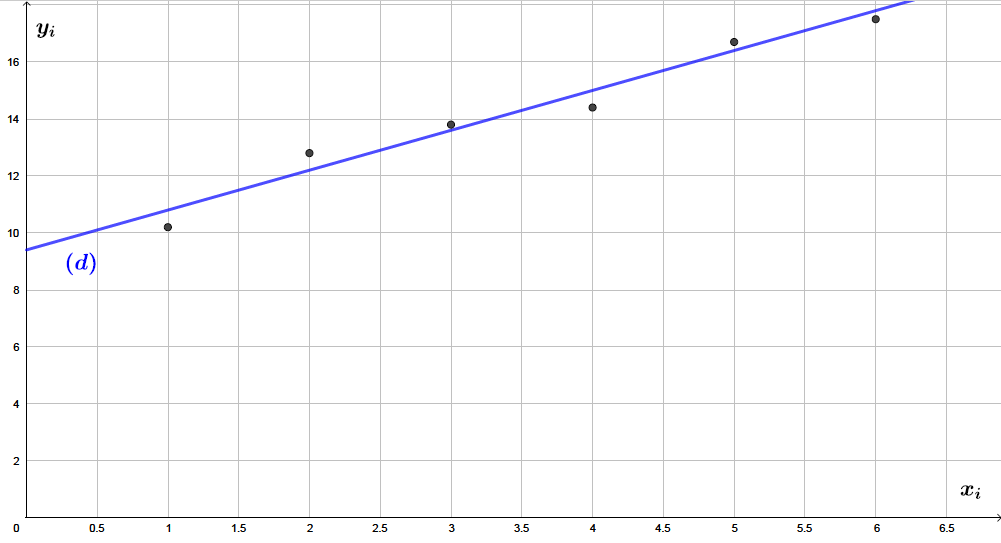
Nous choisissions, par exemple, puis .
Ainsi :
. Le premier point appartenant à la droite admet comme coordonnées .
. Le deuxième point appartenant à la droite admet comme coordonnées .
Il vous suffit de placer ces deux points et ensuite de tracer la droite comme donnée ci-dessous :

Question 5
On suppose que cet ajustement restera valide jusqu’en .
Déterminer le bénéfice en euros que l’on peut prévoir pour l’année .
Déterminer le bénéfice en euros que l’on peut prévoir pour l’année .
Correction
correspond à un rang égal à . On remplace par .
Il vient alors que :
Ainsi :
Le bénéfice que l’on peut estimer avoir en est de milliers d’euros.
Il vient alors que :
Ainsi :
Le bénéfice que l’on peut estimer avoir en est de milliers d’euros.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.