Fonction inverse
Etudes de fonctions - Exercice 2
10 min
15
Soit la fonction définie sur par :
Question 1
Montrer que pour tout réel non nul, on a :
Correction
D'où :
Question 2
Etudier le signe de pour tout réel non nul.
Correction
Nous savons que est un réel non nul.
De ce fait, est alors strictement positif.
Comme alors on peut également dire que
Comme il en résulte donc que :
Finalement, pour tout réel non nul, on peut affirmer que
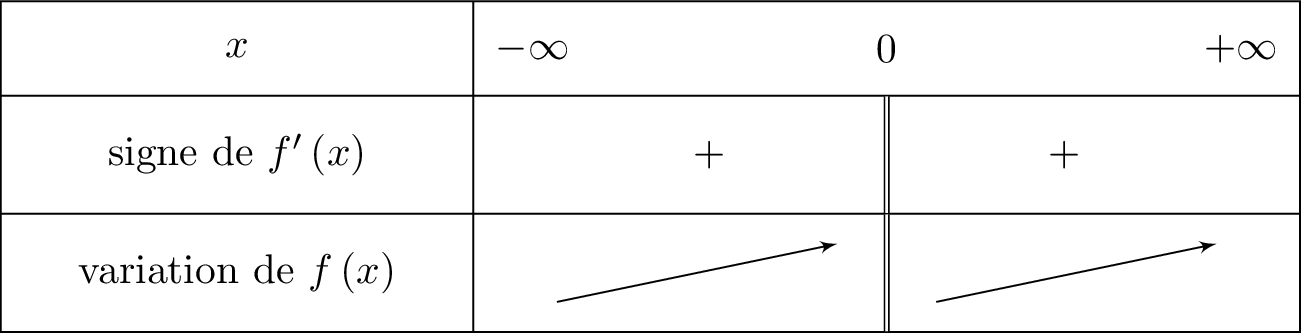
Nous dressons ci-dessous, le tableau de signe de .
De ce fait, est alors strictement positif.
Comme alors on peut également dire que
Comme il en résulte donc que :
Finalement, pour tout réel non nul, on peut affirmer que
Nous dressons ci-dessous, le tableau de signe de .

Question 3
Pour tout réel non nul, en déduire le sens de variation de .
Correction
- Si est négative sur alors est décroissante sur .
- Si est positive sur alors est croissante sur .