Fonction inverse

Etudes de fonctions - Exercice 1

10 min
15
Soit ff la fonction définie sur R∗\mathbb{R^{*}} par : f(x)=−5x+1+2xf\left(x\right)=-5x+1+\frac{2}{x}
Question 1

Montrer que pour tout réel xx non nul, on a : f′(x)=−5−2x2f'\left(x\right)=-5-\frac{2}{x^{2} }

Correction
  • (nombrex)′=−nombrex2\left(\frac{\red{\text{nombre}}}{x} \right)^{'} =-\frac{{\red{\text{nombre}}}}{x^{2} }
    • Nous avons f(x)=−5x+1+2xf\left(x\right)=-5x+1+\frac{\red{2}}{x} alors :
    f′(x)=−5−2x2f'\left(x\right)=-5-\frac{\red{2}}{x^{2} }

    Question 2

    Etudier le signe de f′f' pour tout réel xx non nul.

    Correction
    Nous savons que xx est un réel non nul.
    De ce fait, x2x^{2} est alors strictement positif.
    Comme −2<0-2<0 alors on peut également dire que −2x2<0-\frac{2}{x^{2} }<0
    Comme −5<0-5<0 il en résulte donc que : −5−2x2<0-5-\frac{2}{x^{2} }<0
    Finalement, pour tout réel xx non nul, on peut affirmer que f′(x)<0f'\left(x\right)<0.
    Nous dressons ci-dessous, le tableau de signe de f′f'.
    Question 3

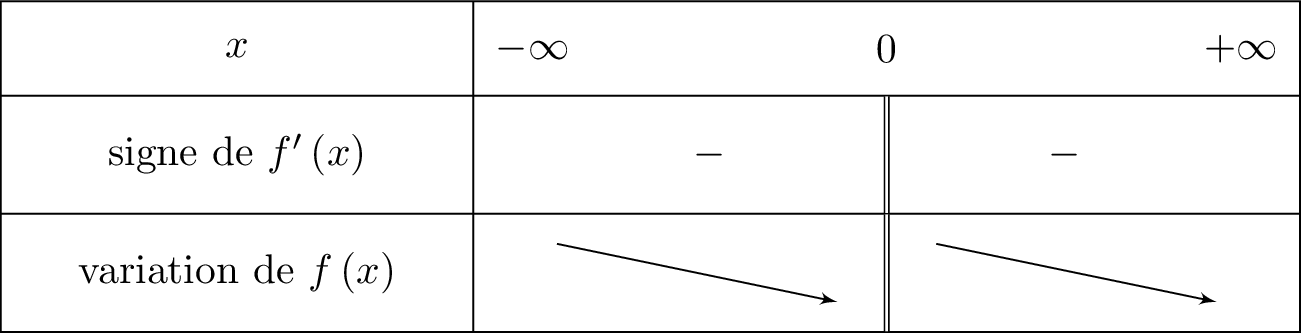
    Pour tout réel xx non nul, en déduire le sens de variation de ff.

    Correction
    • Si f′f' est négative sur [a;b]\left[a;b\right] alors ff est décroissante sur [a;b]\left[a;b\right].
    • Si f′f' est positive sur [a;b]\left[a;b\right] alors ff est croissante sur [a;b]\left[a;b\right].