Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : 2ème partie - Exercice 1
25 min
40
Question 1
Deux ateliers et fabriquent des stylos pour une entreprise.
L’atelier A fabrique des stylos, et parmi ceux-là, possèdent un défaut de fabrication.
De plus, des stylos possèdent un défaut de fabrication et sortent de l’atelier
Un stylo est prélevé au hasard dans le stock de l’entreprise.
On considère les événements suivants :
Le stylo a été fabriqué par l’atelier
Le stylo a été fabriqué par l’atelier
Le stylo possède un défaut de fabrication
L’atelier A fabrique des stylos, et parmi ceux-là, possèdent un défaut de fabrication.
De plus, des stylos possèdent un défaut de fabrication et sortent de l’atelier
Un stylo est prélevé au hasard dans le stock de l’entreprise.
On considère les événements suivants :
Le stylo a été fabriqué par l’atelier
Le stylo a été fabriqué par l’atelier
Le stylo possède un défaut de fabrication
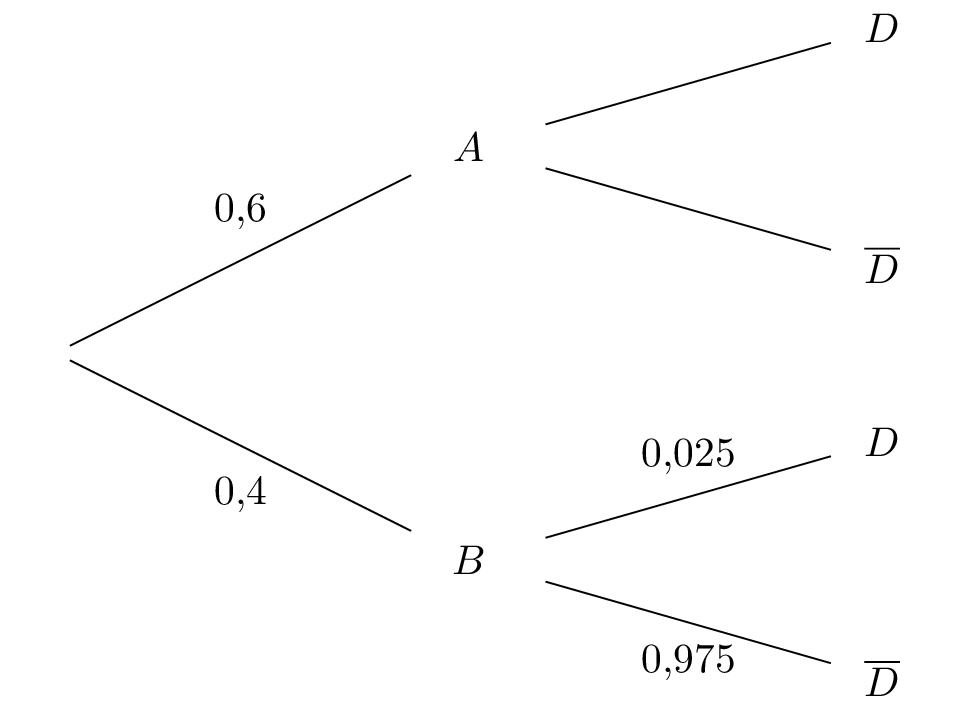
Donner les probabilités , , et .
On pourra s’appuyer sur un arbre de probabilités que l’on complètera au fur et à mesure pour répondre aux questions suivantes.
On pourra s’appuyer sur un arbre de probabilités que l’on complètera au fur et à mesure pour répondre aux questions suivantes.
Correction
Question 2
Calculer la probabilité qu’un stylo provienne de l’atelier et possède un défaut de fabrication.
Correction
La probabilité qu’un stylo provienne de l’atelier possède un défaut de fabrication est notée :
Or à l'aide de l'arbre pondérée ci-dessus, on a :
ON en déduit donc que la probabilité qu’un stylo provienne de l’atelier et possède un défaut de fabrication est de
Or à l'aide de l'arbre pondérée ci-dessus, on a :
ON en déduit donc que la probabilité qu’un stylo provienne de l’atelier et possède un défaut de fabrication est de
Question 3
En déduire que la probabilité qu’un stylo possède un défaut de fabrication est de
Correction
. La probabilité qu’un stylo possède un défaut de fabrication est
Les évènements et forment une partition de l'univers.
D'après la formule des probabilités totales, on a :
équivaut successivement à :
Ainsi :
Les évènements et forment une partition de l'univers.
D'après la formule des probabilités totales, on a :
équivaut successivement à :
Ainsi :
Question 4
On prélève un stylo au hasard dans l’atelier Quelle est la probabilité qu’il possède un défaut ?
Correction
La probabilité qu’il possède un défaut sachant qu’il provient l’atelier B est notée
Il s'agit ici d'une forme avec un "sachant" c'est-à-dire une probabilité conditionnelle.
On peut donner l'arbre de probabilité complet ci-dessous :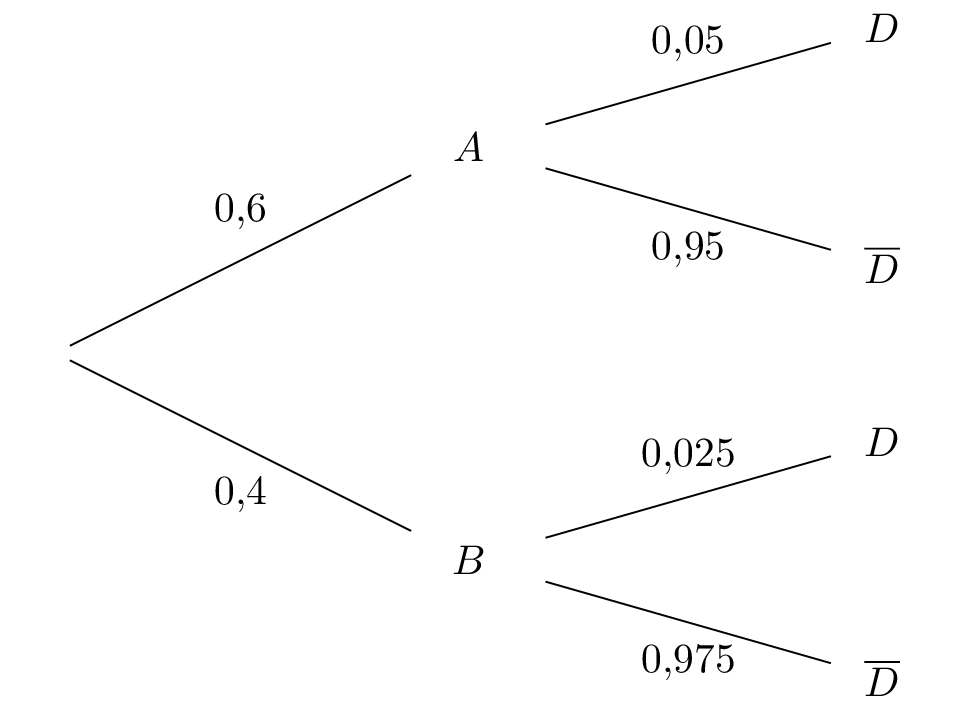
Il s'agit ici d'une forme avec un "sachant" c'est-à-dire une probabilité conditionnelle.
On peut donner l'arbre de probabilité complet ci-dessous :

Question 5
Dans cette partie, on suppose que des stylos possèdent un défaut de fabrication.
L’entreprise confectionne des paquets contenant chacun stylos.
Le fait qu’un stylo possède ou non un défaut de fabrication est indépendant des autres stylos.
On appelle la variable aléatoire donnant pour un paquet le nombre de stylos qui possèdent un défaut de
fabrication.
On admet que la variable aléatoire suit une loi binomiale.
L’entreprise confectionne des paquets contenant chacun stylos.
Le fait qu’un stylo possède ou non un défaut de fabrication est indépendant des autres stylos.
On appelle la variable aléatoire donnant pour un paquet le nombre de stylos qui possèdent un défaut de
fabrication.
On admet que la variable aléatoire suit une loi binomiale.
Préciser les paramètres de cette loi binomiale.
Correction
. Les paramètres de cette loi binomiale sont et
Question 6
Le directeur de l’entreprise affirme qu’il y a plus d’une chance sur deux qu’un paquet ne comporte aucun stylo défectueux. A-t-il raison ?
Correction
La probabilité demandée ici est celle de :
Avec une calculatrice Texas, pour on tape :
2nd - DISTR -- puis choisir
BinomFdp(valeur de n, valeur de p, valeur de k) c'est-à-dire ici BinomFdp(, , ) puis on tape sur enter et on obtient :
Pour certaine version de Texas, on aura BinomPdf au lieu de BinomFdp.
Avec une calculatrice Casio Graph 35+ ou modèle supérieur, pour on tape :
Choisir Menu Stat puis DIST puis BINM et prendre BPD puis VAR.
On remplit le tableau de la manière qui suit :
puis on tape sur EXE et on obtient :
Cette probabilité est ici inférieur à , on peut donc en déduire que le directeur n’a pas raison.
Avec une calculatrice Texas, pour on tape :
2nd - DISTR -- puis choisir
BinomFdp(valeur de n, valeur de p, valeur de k) c'est-à-dire ici BinomFdp(, , ) puis on tape sur enter et on obtient :
arrondi à près.
Pour certaine version de Texas, on aura BinomPdf au lieu de BinomFdp.
Avec une calculatrice Casio Graph 35+ ou modèle supérieur, pour on tape :
Choisir Menu Stat puis DIST puis BINM et prendre BPD puis VAR.
On remplit le tableau de la manière qui suit :
D.P. Binomiale
Data Variable
: Valeur de k
Numtrial : Valeur de
: Valeur de
Data Variable
: Valeur de k
Numtrial : Valeur de
: Valeur de
puis on tape sur EXE et on obtient :
arrondi à près.
Cette probabilité est ici inférieur à , on peut donc en déduire que le directeur n’a pas raison.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.