Les nombres complexes
Module et argument : sous forme de petits problèmes - Exercice 3
20 min
35
Question 1
On donne les nombres complexes suivants et
Donner le module et un argument de .
Correction
Commençons par calculer le module et un argument de .Pour l'argument on sait que :
On a donc
d'où
Avec le cercle trigonométrique on en déduit que ou encore
D'autre part, calculons le module et un argument de .Pour l'argument on sait que :
On a donc
d'où
Avec le cercle trigonométrique on en déduit que ou encore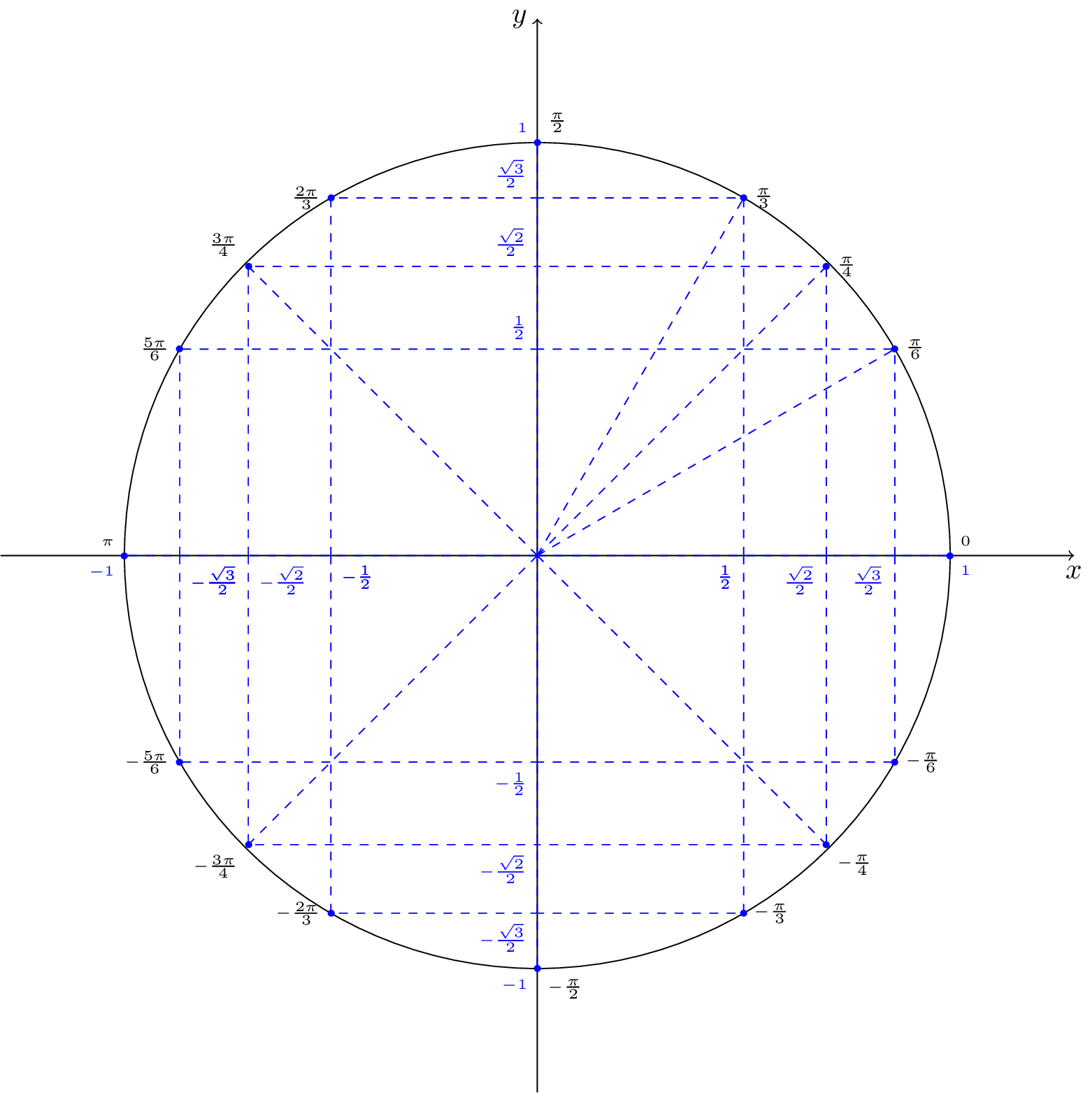
On a donc
d'où
Avec le cercle trigonométrique on en déduit que ou encore
D'autre part, calculons le module et un argument de .
On a donc
d'où
Avec le cercle trigonométrique on en déduit que ou encore

Question 2
Donner le module et un argument de .
Correction
équivaut successivement à :
Question 3
Donner la forme algébrique de .
Correction
équivaut successivement à
D'où :
D'où :
Question 4
En déduire que et
Correction
Soit un nombre complexe dont le module est et un argument de .
- L'écriture trigonométrique de est alors
- L'écriture exponentielle de est alors
En effet : et
Donc l'écriture trigonométrique de est
Comme
et que
Cela signifie que les parties réelles sont égales et les parties imaginaires sont égales, il vient alors que :
et