Les nombres complexes
Exercices types : Encore des classiques - Exercice 2
45 min
65
Question 1
On considère le polynôme défini sur par : .
Démontrer que est une solution de l’équation .
Correction
Il nous faut calculer et vérifier que .
équivaut successivement à :
Ainsi est bien une solution de l’équation .
équivaut successivement à :
Ainsi est bien une solution de l’équation .
Question 2
Démontrer que .
Correction
Nous allons développer l'expression . Ainsi :
. Nous factorisons les expressions en ensemble et les expressions en ensemble.
. Nous factorisons les expressions en ensemble et les expressions en ensemble.
Question 3
En déduire toutes les solutions dans de l’équation .
Correction
Résoudre l'équation revient donc à résoudre l'équation
Il s'agit donc d'une équation produit nul.
D'une part : résolution de l'équation D'autre part : résolution de l'équation , il existe donc deux racines complexes conjuguées notées et tels que et
Finalement les solutions de l'équation sont :
Il s'agit donc d'une équation produit nul.
et
Finalement les solutions de l'équation sont :
Question 4
Le plan complexe est muni d’un repère orthonormé .
On considère les points , et d’affixes respectives ; et
On considère les points , et d’affixes respectives ; et
Déterminer le module et un argument de chacun des trois nombres complexes , et puis les écrire en notation exponentielle.
Correction
On a donc :
Avec le cercle trigonométrique on en déduit que
Il en résulte donc que :
et
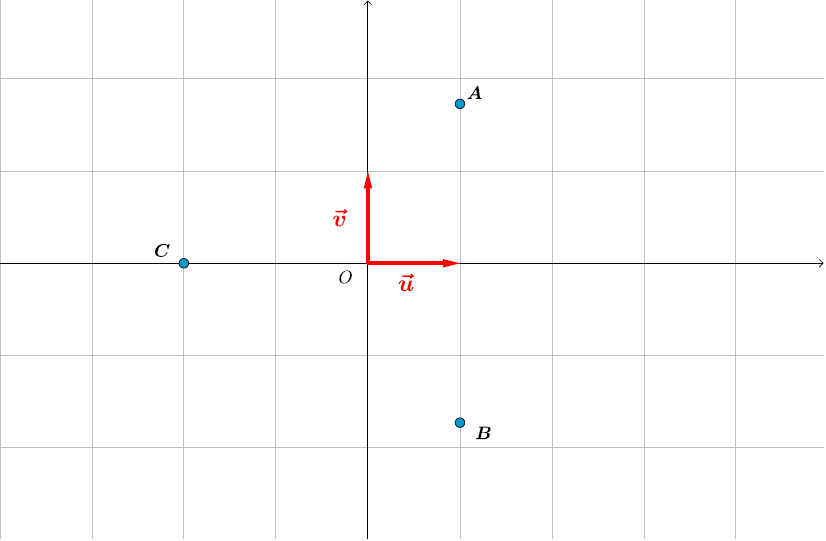
Question 5
Placer les points , et .
Correction
Question 6
On note
Déterminer la forme algébrique de .
Correction
Question 7
Déterminer le module et un argument .
Correction
On a donc :
Avec le cercle trigonométrique on en déduit que
Il en résulte donc que :
Question 8
En déduire la nature du triangle .
Correction
Nous savons que et que
Nous en déduisons les informations suivantes :
et
D'une part :
équivaut successivement à :
. Or : correspond à la distance et correspond à la distance .
Ainsi :
. Il vient alors que :
Le triangle est isocèle en .
D'autre part :
équivaut successivement à :
. Or nous savons également que .
Cela signifie que nous avons un triangle isocèle en et l'angle . Il en résulte donc que les angles à la base et seront égaux car le triangle est isocèle en .
Finalement , le triangle est équilatéral .
Nous en déduisons les informations suivantes :
et
D'une part :
équivaut successivement à :
. Or : correspond à la distance et correspond à la distance .
Ainsi :
. Il vient alors que :
.
Le triangle est isocèle en .
D'autre part :
équivaut successivement à :
Cela signifie que nous avons un triangle isocèle en et l'angle . Il en résulte donc que les angles à la base et seront égaux car le triangle est isocèle en .
Finalement , le triangle est équilatéral .
Question 9
À tout point d’affixe (avec ), on associe le point d’affixe défini par : .
On remarquera que :
On remarquera que :
Démontrer que si le point appartient à la médiatrice du segment alors le point appartient à un cercle dont on précisera le centre et le rayon.
Correction
Si le point appartient à la médiatrice du segment , cela signifie donc que .
Autrement dit , il faut que :
Comme on vient de voir, si le point appartient à la médiatrice du segment cela est équivalent à
Or correspond à la distance . Comme alors .
appartient donc au cercle de centre de rayon .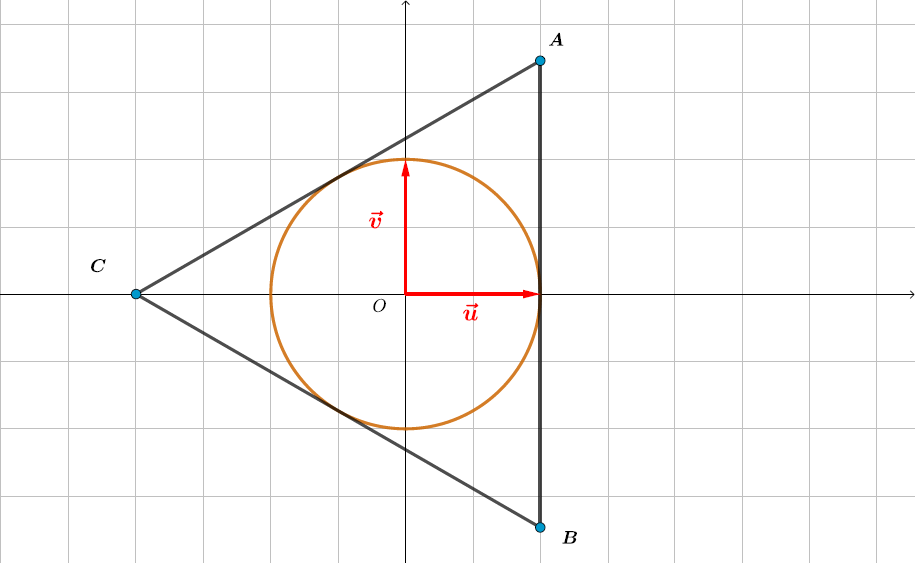
Autrement dit , il faut que :
Comme on vient de voir, si le point appartient à la médiatrice du segment cela est équivalent à
Or correspond à la distance . Comme alors .
appartient donc au cercle de centre de rayon .

Question 10
Démontrer que si appartient au cercle de diamètre privé de alors appartient à l’axe .
Correction
On sait que si appartient au cercle de diamètre privé de alors :
ou
Ainsi est un imaginaire pur ce qui signifie que appartient à l’axe .
ou
Ainsi est un imaginaire pur ce qui signifie que appartient à l’axe .