Les nombres complexes
Exercices types : Des classiques - Exercice 2
25 min
45
Question 1
On note l'ensemble des nombres complexes.
On munit le plan complexe d'un repère orthonormé direct .
On considère la fonction qui à tout nombre complexe associe .
On munit le plan complexe d'un repère orthonormé direct .
On considère la fonction qui à tout nombre complexe associe .
Calculer l'image de par la fonction .
Correction
Question 2
Résoudre dans l'équation .
Correction
équivaut successivement à :
Lorsque nous devons résoudre une équation qui fait intervenir du , on utilisera le discriminant.
Pour les cas et , on effectuera la même démarche vue en classe de première.
Cependant pour , il y aura deux racines complexes conjuguées notées et tels que
et .
,il existe donc deux racines complexes conjuguées notées et tels que et
Donc
Lorsque nous devons résoudre une équation qui fait intervenir du , on utilisera le discriminant.
et
,il existe donc deux racines complexes conjuguées notées et tels que et
et
Donc
Question 3
Soit un nombre réel. On considère l'équation d'inconnue .
Déterminer l'ensemble des valeurs de pour lesquelles admet deux solutions complexes conjuguées.
Correction
équivaut successivement à :
Pour que l’équation admette deux solutions complexes conjuguées, il faut que le discriminant du polynôme soit strictement négatif.
Si alors l’équation admet deux solutions complexes conjuguées.
Pour que l’équation admette deux solutions complexes conjuguées, il faut que le discriminant du polynôme soit strictement négatif.
Si alors l’équation admet deux solutions complexes conjuguées.
Question 4
Soit l’ensemble des points du plan complexe dont l’affixe vérifie .
Prouver que est le cercle de centre et de rayon .
Correction
équivaut successivement à :
On pose ainsi
Il en résulte que
L'ensemble des points du plan tel que est le cercle de centre et de rayon .
Question 5
Soit un nombre complexe, tel que où et sont des nombres réels.
Montrer que la forme algébrique de est : .
Correction
équivaut successivement à :
Question 6
On note l’ensemble des points du plan complexe dont l’affixe est telle que soit un nombre réel.
Montrer que est la réunion de deux droites et dont on précisera les équations.
Correction
est un nombre réel si et seulement si sa partie imaginaire est nulle.
Or :
Il faut donc que
On factorise par
On reconnait une équation produit nul.
Soit :
ou
ou
ou
ou
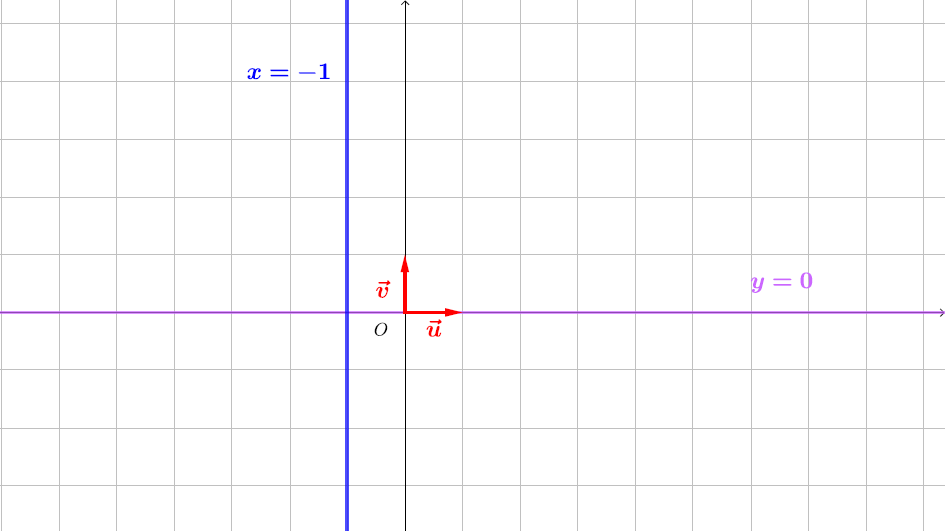
Donc est la réunion de deux droites d’équation (l’axe des abscisses) et d’équation .
Or :
Il faut donc que
On factorise par
On reconnait une équation produit nul.
Soit :
ou
ou
ou
ou
Donc est la réunion de deux droites d’équation (l’axe des abscisses) et d’équation .
