Les nombres complexes
Des complexes et des suites : A la mode au BAC - Exercice 4
40 min
65
Question 1
On définit la suite de nombres complexes de la manière suivante : et, pour tout entier naturel , .
On travaille dans le plan complexe rapporté au repère orthonormal direct .
Pour tout entier naturel , on note le point du plan d’affixe .
Pour tout entier naturel , on pose et on note le point d’affixe . On note le point d’affixe .
On travaille dans le plan complexe rapporté au repère orthonormal direct .
Pour tout entier naturel , on note le point du plan d’affixe .
Pour tout entier naturel , on pose et on note le point d’affixe . On note le point d’affixe .
Exprimer en fonction de , pour tout entier naturel .
Correction
est une suite géométrique de raison et de premier terme . Ainsi le premier terme .
Question 2
Démontrer que, pour tout entier naturel , on a :
Correction
Nous avons vu a la question précédente, que est une suite géométrique de raison et de premier terme .
Ainsi :
- L'expression de en fonction de est donnée par la formule
Question 3
Pour tout entier naturel , calculer, en fonction de , le module de .
Correction
Nous savons maintenant que :
Question 4
Démontrer que
Correction
D'après la question précédente, on a vu que :
Or donc . De ce fait :
D'où :
Comme alors :
Ainsi :
Or donc . De ce fait :
D'où :
- Si alors .
- Si alors .
Ainsi :
Question 5
Quelle interprétation géométrique peut-on donner de ce résultat?
Correction
est l’affixe du point , et est l’affixe du point .
Le module correspond géométriquement à la distance .
Comme cela signifie que lorsque tend vers , la distance entre le point et le point sera nulle.
Le module correspond géométriquement à la distance .
Comme cela signifie que lorsque tend vers , la distance entre le point et le point sera nulle.
Question 6
Soit un entier naturel. déterminer un argument de .
Correction
Nous savons que . Comme est un réel alors :
Notons . Nous allons déterminer le module puis l'argument de .
L'argument de est donné par
Avec le cercle trigonométrique on en déduit que
Il en résulte donc que :
Notons . Nous allons déterminer le module puis l'argument de .
L'argument de est donné par
Avec le cercle trigonométrique on en déduit que
Il en résulte donc que :
Question 7
Démontrer que, lorsque décrit l’ensemble des entiers naturels, les points sont alignés.
Correction
Les points ont pour affixes les nombres un dont l’argument est constant à près.
Pour tout , chaque point appartient à la droite d’équation ; donc tous les points sont alignés.
Nous avons représenté ci-dessous tous les points dont l'argument sera toujours égal à .
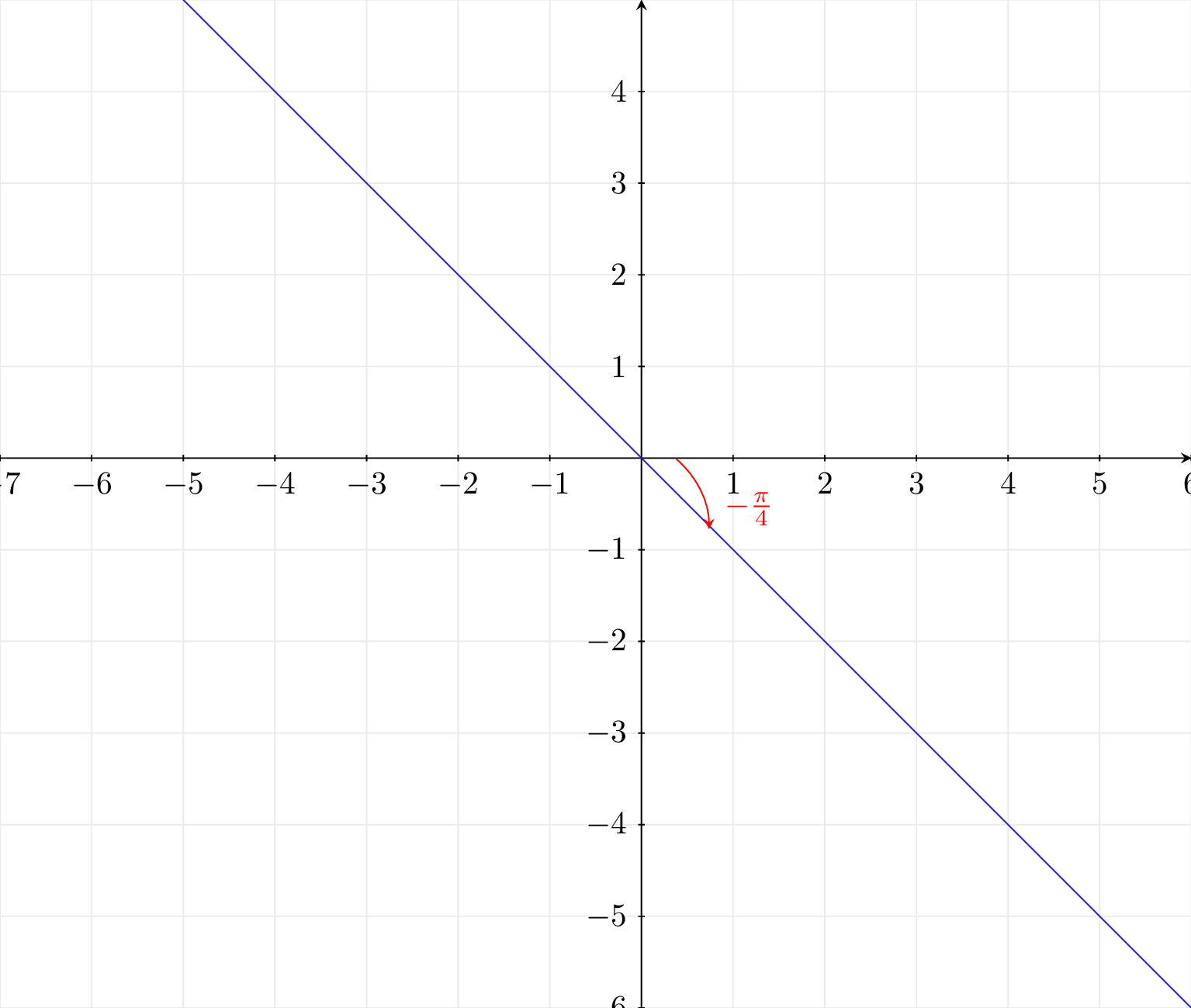
Pour tout , chaque point appartient à la droite d’équation ; donc tous les points sont alignés.
Nous avons représenté ci-dessous tous les points dont l'argument sera toujours égal à .

Question 8
Démontrer que, pour tout entier naturel , le point appartient à la droite d’équation réduite :
Correction
Nous savons que et également que .
Il en résulte donc que :
Ainsi :
Nous allons appeler la partie réelle de et la partie imaginaire de .
Il vient alors que :
et que l'on peut aussi écrire car .
Finalement, le point appartient à la droite d’équation réduite :
Il en résulte donc que :
Ainsi :
Nous allons appeler la partie réelle de et la partie imaginaire de .
Il vient alors que :
et que l'on peut aussi écrire car .
Finalement, le point appartient à la droite d’équation réduite :