Les nombres complexes

Des complexes et des suites : A la mode au BAC - Exercice 2

30 min
45
On considère la suite de nombres complexes (zn)\left(z_{n}\right) définie par z0=3−iz_{0}=\sqrt{3}-i et pour tout entier naturel nn, zn+1=(1+i)znz_{n+1}=\left(1+i\right)z_{n}
Question 1
Pour tout entier naturel nn, on pose un=∣zn∣u_{n} =\left|z_{n} \right|

Calculer u0u_{0}.

Correction
Nous avons : u0=∣z0∣u_{0} =\left|z_{0} \right|
Ainsi :
∣z0∣=∣3−i∣\left|z_{0} \right|=\left|\sqrt{3}-i \right| équivaut successivement à :
∣z0∣=(3)2+(−1)2\left|z_{0} \right|=\sqrt{\left(\sqrt{3} \right)^{2} +\left(-1\right)^{2} }
∣z0∣=3+1\left|z_{0} \right|=\sqrt{3+1}
∣z0∣=4\left|z_{0} \right|=\sqrt{4}
∣z0∣=2\left|z_{0} \right|=2
Question 2

Démontrer que (un)\left(u_{n}\right) est une suite géométrique de raison 2\sqrt{2} et de premier terme 22.

Correction
un=∣zn∣u_{n} =\left|z_{n} \right|
un+1=∣zn+1∣u_{n+1} =\left|z_{n+1} \right|
un+1=∣(1+i)zn∣u_{n+1} =\left|\left(1+i\right)z_{n} \right|
un+1=∣1+i∣×∣zn∣u_{n+1} =\left|1+i\right|\times \left|z_{n} \right|
un+1=12+12×∣zn∣u_{n+1} =\sqrt{1^{2} +1^{2} } \times \left|z_{n} \right|
un+1=2×∣zn∣u_{n+1} =\sqrt{2 } \times \left|z_{n} \right| . Or un=∣zn∣u_{n} =\left|z_{n} \right|. Il vient alors que :
un+1=2×unu_{n+1} =\sqrt{2} \times u_{n}

(un)\left(u_{n}\right) est une suite géométrique de raison 2\sqrt{2} et de premier terme u0=∣z0∣u_{0} =\left|z_{0} \right| que l'on a calculé à la question 11. Ainsi le premier terme u0=2u_{0} =2.
Question 3

Pour tout entier naturel nn, exprimer unu_{n} en fonction de nn.

Correction
D'après la question précédente, on a vu que (un)\left(u_{n}\right) est une suite géométrique de raison 2\sqrt{2} et de premier terme u0=2u_{0} =2.
  • L'expression de unu_{n} en fonction de nn est donnée par la formule
    un=u0×qnu_{n} =u_{0} \times q^{n}

Ainsi :
un=2×(2)nu_{n} =2\times \left(\sqrt{2} \right)^{n}
Question 4

Déterminer la limite de la suite (un)\left(u_{n}\right).

Correction
  • Si −1<q<1-1<q<1 alors lim⁡n→+∞qn=0\lim\limits_{n\to +\infty } q^{n} =0.
  • Si q>1 q >1 alors lim⁡n→+∞qn=+∞\lim\limits_{n\to +\infty } q^{n} =+\infty.
Comme 2>1\sqrt{2} >1 alors :
lim⁡n→+∞(2)n=+∞\lim\limits_{n\to +\infty } \left(\sqrt{2}\right)^{n} =+\infty
lim⁡n→+∞2×(2)n=+∞\lim\limits_{n\to +\infty } 2\times\left(\sqrt{2}\right)^{n} =+\infty
Ainsi :
lim⁡n→+∞un=+∞\lim\limits_{n\to +\infty } u_{n} =+\infty
Question 5
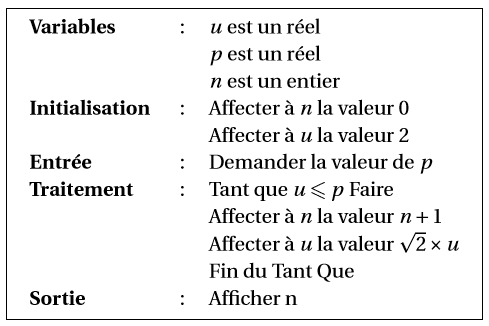
Étant donné un réel positif pp, on souhaite déterminer, à l’aide d’un algorithme, la plus petite valeur de l’entier naturel nn telle que un>pu_{n}>p.

Recopier l’algorithme ci-dessous et le compléter par les instructions de traitement et de sortie, de façon à afficher la valeur cherchée de l’entier nn.

Correction