Bac 2025
🔮 Découvre nos pronostics sur les exercices qui risquent de tomber cette année !Regarder la vidéo →
Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Complexes : médiatrices et cercles - Exercice 1
15 min
20
Dans chacun des cas suivants, déterminez l'ensemble des points du plan complexe dont l'affixe vérifie la condition donnée.
Regardez la vidéo Cercle et Médiatrice pour vous aider.
Regardez la vidéo Cercle et Médiatrice pour vous aider.
Question 1
Correction
Soit le point d'affixe .
On pose ainsi
Il en résulte que
L'ensemble des points du plan tel que est le cercle de centre et de rayon .
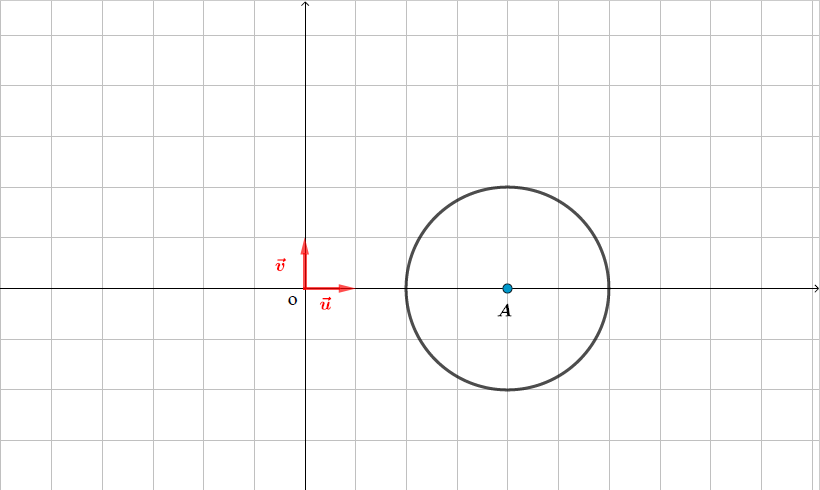
On pose ainsi
Il en résulte que
L'ensemble des points du plan tel que est le cercle de centre et de rayon .

Question 2
Correction
Soit le point d'affixe .
On pose ainsi
Il en résulte que
L'ensemble des points du plan tel que est le cercle de centre et de rayon .
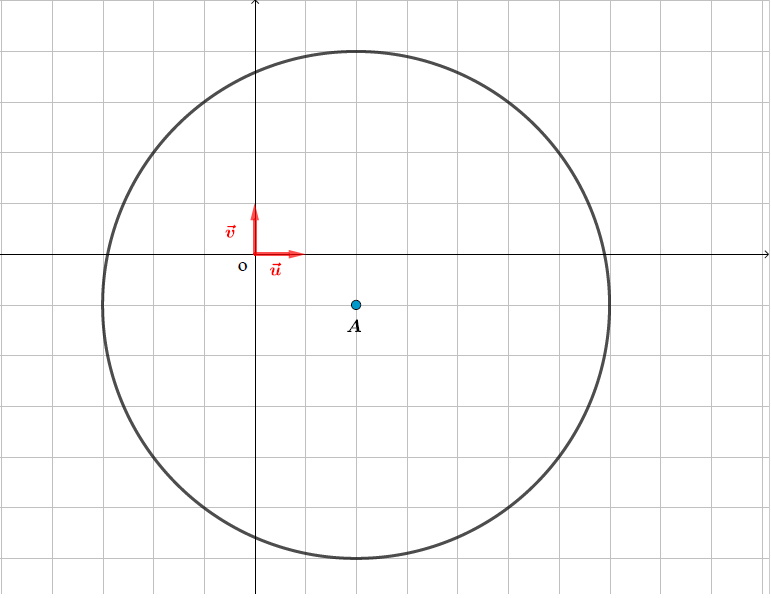
On pose ainsi
Il en résulte que
L'ensemble des points du plan tel que est le cercle de centre et de rayon .

Question 3
Correction
Soit le point d'affixe .
On pose et ainsi
Il en résulte que
L'ensemble des points du plan tel que est la médiatrice du segment
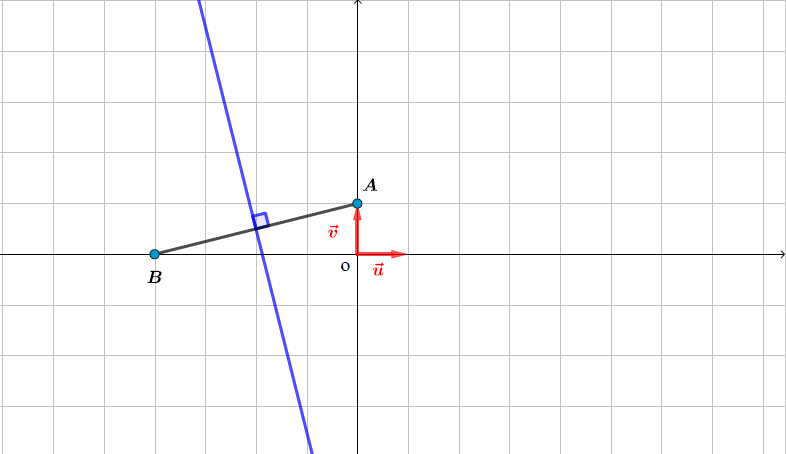
On pose et ainsi
Il en résulte que
L'ensemble des points du plan tel que est la médiatrice du segment

Question 4
Correction
Soit le point d'affixe .
On pose et ainsi
Il en résulte que
L'ensemble des points du plan tel que est la médiatrice du segment
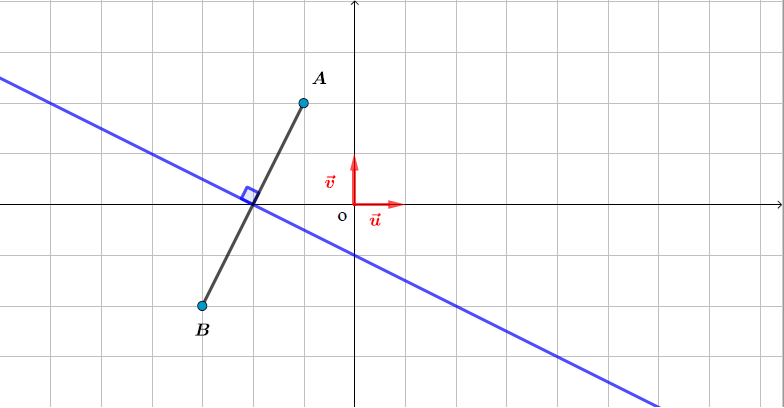
On pose et ainsi
Il en résulte que
L'ensemble des points du plan tel que est la médiatrice du segment

Question 5
Correction
Soit le point d'affixe .
équivaut successivement à :
On pose et ainsi
Il en résulte que
L'ensemble des points du plan tel que est la médiatrice du segment .
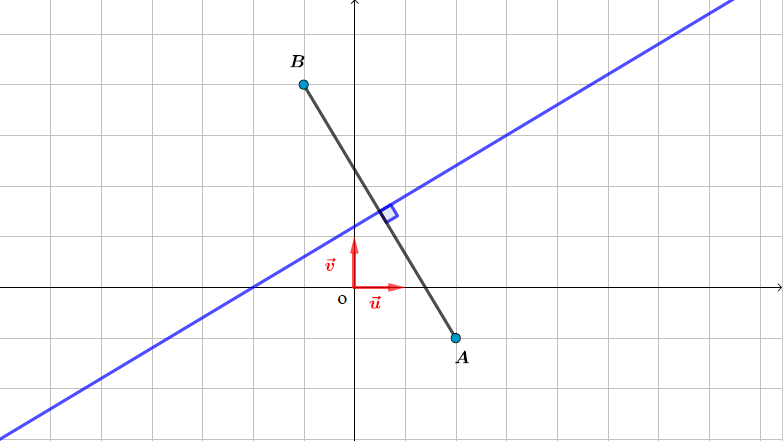
On pose et ainsi
Il en résulte que
L'ensemble des points du plan tel que est la médiatrice du segment .

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.