QCM - Exercice 2

20 min
35
Question 1
Cet exercice est un questionnaire à choix multiples (Q.C.M.). Pour chacune des questions, une seule des quatre réponses est exacte.

Une variable aléatoire XX suit la loi normale de moyenne 100100 et d’écart-type 3636. Les résultats sont données à 10−310^{-3} près.
  • P(X≤81,2)≈0,542P\left(X\le 81,2\right)\approx0,542
  • P(X≤81,2)≈0,301P\left(X\le 81,2\right)\approx0,301
  • P(81,2≤X≤103,8)≈0,542P\left(81,2\le X\le 103,8\right)\approx0,542
  • P(81,2≤X≤103,8)≈0,301P\left(81,2\le X\le 103,8\right)\approx0,301

Correction
La bonne réponse est a.
On calcule à la calculatrice la probabilité P(X≤81,2)P\left(X\le 81,2\right) et on obtient environ 0,3007580,300758 ce qui donc 0,3010,301 à 10−310^{-3} près.
Avec une calculatrice Texas, pour P(X≤81,2)P\left(X\le 81,2\right) on tape NormalFrep(valeur min, valeur max, espérance, écart type)
C'est-à-dire ici NormalFrep(−1099-10^{99}, 81.281.2 , 100100, 3636) puis on tape sur Enter on obtient :
P(X≤81,2)≈0,301P\left(X\le 81,2\right)\approx 0,301

Avec une calculatrice Casio Graph 35+, pour P(X≤81,2)P\left(X\le 81,2\right) on tape :
Normal C.D
Lower : −1099-10^{99} valeur Minimale
Upper : 81.281.2 valeur Maximale
σ\sigma : 100100 écart type
μ\mu : 3636 espérance

puis on tape sur EXE et on obtient :
P(X≤81,2)≈0,301P\left(X\le 81,2\right)\approx 0,301
Question 2

Une variable aléatoire XX suit la loi normale de moyenne 5050 et d’écart-type 22.
Une variable aléatoire NN suit la loi normale centrée réduite. On a alors :
  • P(X>52)=1−P(−2<N<2)2P\left(X>52\right)=\frac{1-P\left(-2<N<2\right)}{2}
  • P(X>52)=1−P(−2<N<2)P\left(X>52\right)=1-P\left(-2<N<2\right)
  • P(X>52)=1−P(−1<N<1)2P\left(X>52\right)=\frac{1-P\left(-1<N<1\right)}{2}
  • P(X>52)=P(N≥1)P\left(X>52\right)=P\left(N\ge1\right)

Correction
La bonne réponse est d.

Si une variable aléatoire XX suit une loi normale de paramètres μ\mu et σ\sigma notée N(μ;σ2)N\left(\mu;\sigma ^{2} \right), alors la variable aléatoire Z=X−μσZ=\frac{X-\mu }{\sigma} suit une loi normale centrée réduite N(0;1)N\left(0;1\right)
Nous savons que XX est une variable aléatoire qui suit la loi normale de moyenne μ=50\mu=50 et d’écart-type σ=2\sigma=2.
On pose alors N=X−502N=\frac{X-50}{2} qui suit la loi normale centrée réduite N(0;1)N\left(0;1\right).
Il vient alors que :
P(X>52)=P(X−502>52−502)P\left(X> 52 \right)=P\left(\frac{X-50}{2}> \frac{52-50}{2} \right)
P(X>52)=P(X−502>1)P\left(X> 52 \right)=P\left(\frac{X-50}{2}> 1 \right)
P(X>52)=P(N>1)P\left(X> 52 \right)=P\left(N> 1 \right)
Puisque la loi normale et une loi continue, on sait que la probabilité d’une issue isolée est nulle, donc :
P(X>52)=P(N>1)=P(N≥1)P\left(X> 52 \right)=P\left(N> 1 \right)=P\left(N\ge 1 \right)
Question 3

Une variable aléatoire TT suit une loi exponentielle telle que P(T>2)=0,5P\left(T>2\right)=0,5. Une valeur approchée à 10−210^{-2} près de PT>2(T>5)P_{T> 2} \left(T> 5\right) est égale à :
  • 0,350,35
  • 0,540,54
  • 0,530,53
  • e2\frac{e}{2}

Correction
La bonne réponse est a.
1ère étape : On détermine le paramètre λ\lambda de la loi exponentielle à l'aide de P(T>2)=0,5P\left(T>2\right)=0,5

La fonction de densité de probabilité de la loi exponentielle sur [0;+∞[\left[0;+\infty \right[ est f(x)=λe−λxf\left(x\right)=\lambda e^{-\lambda x} où λ\lambda est un réel positif.
  • P(a≤X≤b)=∫abλe−λxdx=[−e−λx]ab=e−λa−e−λbP\left(a\le X\le b\right)=\int _{a}^{b}\lambda e^{-\lambda x} dx=\left[-e^{-\lambda x} \right] _{a}^{b} =e^{-\lambda a} -e^{-\lambda b}
  • P(X≤a)=P(0≤X≤a)=∫0aλe−λxdx=[−e−λx]0a=1−e−λaP\left(X\le a\right)=P\left(0\le X\le a\right)=\int _{0}^{a}\lambda e^{-\lambda x} dx=\left[-e^{-\lambda x} \right] _{0}^{a} =1-e^{-\lambda a}
  • P(X≥a)=1−P(X≤a)=1−(1−e−λa)=e−λaP\left(X\ge a\right)=1-P\left(X\le a\right)=1-\left(1-e^{-\lambda a} \right)=e^{-\lambda a}
On sait que : P(T>2)=0,5P\left(T>2\right)=0,5 ce qui donne alors : e−2λ=0,5e^{-2\lambda } =0,5
Il en résulte donc que :
e−2λ=0,5e^{-2\lambda } =0,5 (voir la vidéo sur les équations exponentielles si besoin)
e−2λ=0,5e^{-2\lambda } =0,5 équivaut successivement à
e−2λ=eln⁡(0,5)e^{-2\lambda } =e^{\ln \left(0,5\right)}
−2λ=ln⁡(0,5)-2\lambda =\ln \left(0,5\right)
−2λ=ln⁡(12)-2\lambda =\ln \left(\frac{1}{2} \right)
−2λ=−ln⁡(2)-2\lambda =-\ln \left(2 \right)
Ainsi :
λ=ln⁡(2)2\lambda =\frac{\ln \left(2\right)}{2}

2ème étape : Calculons maintenant PT>2(T>5)P_{T> 2} \left(T> 5\right)

La loi exponentielle est une loi sans vieillissement ou sans mémoire c'est-à-dire que :
∀t>0\forall t>0 et h>0h>0 on a PX≥t(X≥t+h)=P(X≥h)P_{X\ge t} \left(X\ge t+h\right)=P\left(X\ge h\right)
Il en résulte que d'après l'énoncé, on cherche à calculer :
PT>2(T>5)=PT≥2(T≥2+3)P_{T> 2} \left(T> 5\right)=P_{T\ge 2} \left(T\ge 2+3\right)
Donc d'après la formule ci-dessous :
PT>2(T>5)=P(T≥3)P_{T> 2} \left(T> 5\right)=P\left(T\ge 3\right)
On a :
P(T≥3)=e−3λP\left(T\ge 3\right)=e^{-3\lambda } équivaut successivement à :
P(T≥3)=e−3×ln⁡(2)2P\left(T\ge 3\right)=e^{-3\times \frac{\ln \left(2\right)}{2}}
P(T≥3)≈0,353P\left(T\ge 3\right)\approx 0,353
D'où :
PT>2(T>5)≈0,353P_{T> 2} \left(T> 5\right)\approx 0,353
Question 4
Une urne contient 55 boules bleues et 33 boules grises indiscernables au toucher. On tire successivement de manière indépendante 55 boules avec remise dans cette urne. On note alors XX la variable aléatoire comptant le nombre de boules grises tirées.

On note E(X)E\left(X\right) l’espérance de XX. On a alors :
  • 33
  • 38\frac{3}{8}
  • P(X≥1)≈0,905P\left(X\ge 1\right)\approx0,905 à 10−310^{-3} près
  • P(X≥1)≈0,095P\left(X\ge 1\right)\approx0,095 à 10−310^{-3} près

Correction
La bonne réponse est c.
A chaque tirage la probabilité de tirer une boule grise est de 38\frac{3}{8}
On est donc en présence d'un schéma de Bernoulli :
On appelle succès "tirer une boule grise" avec la probabilité p=38p=\frac{3}{8}
On appelle échec "tirer une boule bleue" avec la probabilité 1−p=581-p=\frac{5}{8}
On répète cinq fois de suite cette expérience de façon indépendante.
XX est la variable aléatoire qui associe le nombre de fois que l'on tire une boule grise.
XX suit la loi binomiale de paramètre n=5n=5 et p=38p=\frac{3}{8}
On note alors X∼B(5;38)X \sim B\left(5;\frac{3}{8} \right)
XX est une variable aléatoire qui suit une loi binomiale B(n,p)B\left(n, p\right), alors l’espérance mathématique E(X)E\left(X\right), la variance V(X)V\left(X\right) et l’écart type σ(X)\sigma\left(X\right) sont égales à :
  • E(X)=n×pE\left(X\right)=n\times p
    • Ainsi :
    E(X)=5×38E\left(X\right)=5\times \frac{3}{8} donc
    E(X)=1,875E\left(X\right)=1,875
    On rejette donc la proposition aa et bb.
    Pour le calcul de P(X≥1)P\left(X\ge1\right) nous écrivons alors que : P(X≥1)=1−P(X=0)P\left(X\ge1\right)=1-P\left(X=0\right)
    Pour le calcul de P(X=0)P\left(X=0\right) :
    Avec une calculatrice Texas, pour P(X=0)P\left(X=0\right) on tape :
    (tu peux regarder la fiche "Utiliser la loi binomiale avec une Texas" pour plus de détails)
    2nd - DISTR -- puis choisir
    BinomFdp(valeur de n, valeur de p, valeur de k) c'est-à-dire ici BinomFdp(55, 38\frac{3}{8} , 00) puis on tape sur enter et on obtient :
    P(X=0)≈0,095P\left(X=0\right)\approx 0,095
    arrondi à 10−310^{-3} près.
    Pour certaines versions de Texas, on aura BinomPdf au lieu de BinomFdp.
    Enfin : P(X≥1)=1−P(X=0)P\left(X\ge 1\right)=1-P\left(X=0\right)
    Soit : P(X≥1)=1−P(X=0)P\left(X\ge 1\right)=1-P\left(X=0\right)
    D'où :
    P(X≥1)≈1−0,095≈0,905P\left(X\ge 1\right)\approx 1-0,095 \approx 0,905

    Avec une calculatrice Casio Graph 35+ ou modèle supérieur , pour P(X=0)P\left(X=0\right) :
    (tu peux regarder la fiche "Utiliser la loi binomiale avec une Casio" pour plus de détails)
    Choisir Menu Stat puis DIST puis BINM et prendre BPD puis VAR.
    On remplit le tableau de la manière qui suit :
    D.P. Binomiale
    Data Variable
    xx : 00 Valeur de kk
    Numtrial : 55 Valeur de nn
    pp : 38\frac{3}{8} Valeur de pp

    puis on tape sur EXE et on obtient :
    P(X=0)≈0,095P\left(X=0\right)\approx 0,095
    arrondi à 10−310^{-3} près.
    Enfin : P(X≥1)=1−P(X=0)P\left(X\ge 1\right)=1-P\left(X=0\right)
    Soit : P(X≥1)=1−P(X=0)P\left(X\ge 1\right)=1-P\left(X=0\right)
    D'où :
    P(X≥1)≈1−0,095≈0,905P\left(X\ge 1\right)\approx 1-0,095 \approx 0,905
    Question 5
    La fonction ff est la fonction densité de probabilité associée à la loi normale centrée réduite N(0;1)N\left(0;1 \right).
    La fonction gg est la fonction de densité de probabilité associée à la loi normale de moyenne μ=3\mu=3 et d’écart-type σ=2\sigma=2.

    La représentation graphique de ces deux fonctions est :

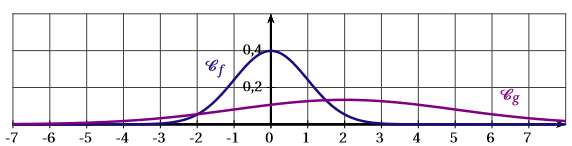
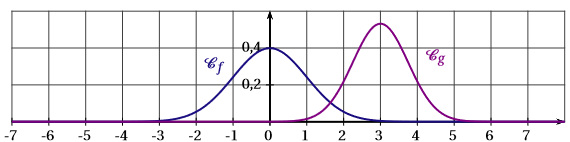
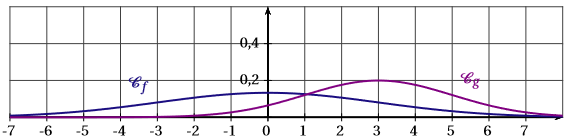
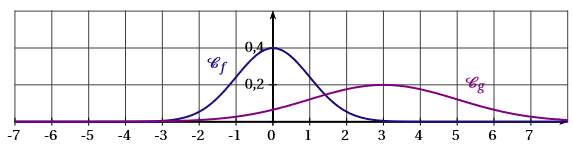
    Correction
    La bonne réponse est d.
    • La fonction ff est la fonction de Gauss définie par f(x)=12πe−x22f\left(x\right)=\frac{1}{\sqrt{2\pi } } e^{-\frac{x^{2} }{2} }. Ainsi : f(x)=12π≈0,4f\left(x\right)=\frac{1}{\sqrt{2\pi } }\approx0,4 ce qui exclu automatiquement la courbe c.
    • La courbe représentative de gg doit être symétrique par rapport à la droite d’équation x=μ=3x=\mu=3; cela exclut la courbe a.
    • On sait également que : P(μ−σ≤X≤μ+σ)=P(1≤X≤5)≈0,68P\left(\mu -\sigma \le X\le \mu +\sigma \right)=P\left(1\le X\le 5\right)\approx 0,68. Cela exclut la figure b, car l’aire correspondante entre x=1x=1 et x=5x=5 est visiblement supérieure à quatre carreaux, donc supérieure à 0,80,8.
    La bonne réponse est donc d.
    Question 6

    Dans un restaurant, le temps d’attente pour être servi, exprimé en minute, peut être modélisé par une variable aléatoire XX qui suit la loi uniforme sur l’intervalle [0;16]\left[0;16\right]. Quelle est le temps d'attente moyen ?
    • 77
    • 7,57,5
    • 88
    • 8,58,5

    Correction
    La bonne réponse est c.

    Si XX suit la loi uniforme sur un intervalle [a,b]\left[a,b\right] alors son espérance mathématique vaut E(X)=a+b2E\left(X\right)=\frac{a+b}{2}
    Il en résulte que :
    E(X)=0+162=8E\left(X\right)=\frac{0+16}{2} =8

    Le temps d'attente pour être servi est de 88 minutes.

    Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.