La géométrie dans l'espace et produit scalaire
Repères et coordonnées - Exercice 2
15 min
25
On considère un cube .
L'espace est rapporté au repère orthonormé .
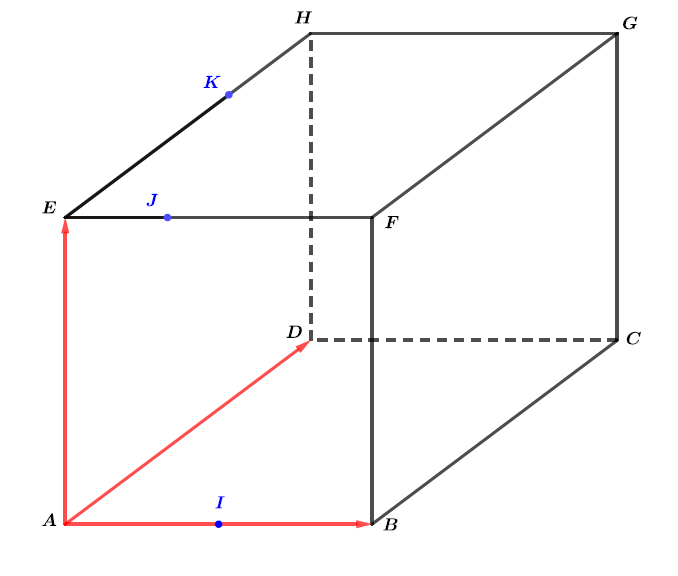
L'espace est rapporté au repère orthonormé .

- Le point est le milieu de
- Le point vérifie la relation
- Le point vérifie la relation
Question 1
Déterminer les coordonnées des points , , et .
Correction
est l'origine du repère ainsi
donc les coordonnées de sont
donc les coordonnées de sont
donc les coordonnées de sont
donc les coordonnées de sont
donc les coordonnées de sont
milieu de ainsi les coordonnées de sont
On va maintenant donner les coordonnées de et .
L'objectif est d'écrire par exemple que
On a :
donc les coordonnées de sont
On a également
équivaut successivement à
donc les coordonnées de sont
donc les coordonnées de sont
donc les coordonnées de sont
donc les coordonnées de sont
donc les coordonnées de sont
donc les coordonnées de sont
milieu de ainsi les coordonnées de sont
On va maintenant donner les coordonnées de et .
L'objectif est d'écrire par exemple que
On a :
donc les coordonnées de sont
On a également
équivaut successivement à
donc les coordonnées de sont
Question 2
Montrer que les droites et sont parallèles.
Correction
On souhaite montrer si les droites et sont parallèles.
On connaît les coordonnées de et .
Si les vecteurs et colinéaires alors les et seront bien parallèles
On sait les coordonnées des points suivants ; ; et
On calcule les vecteurs et
Existe-t-il un réel tel que ?
On obtient le système suivant
Ainsi
Il en résulte que .
Les vecteurs et sont colinéaires alors les et sont bien parallèles.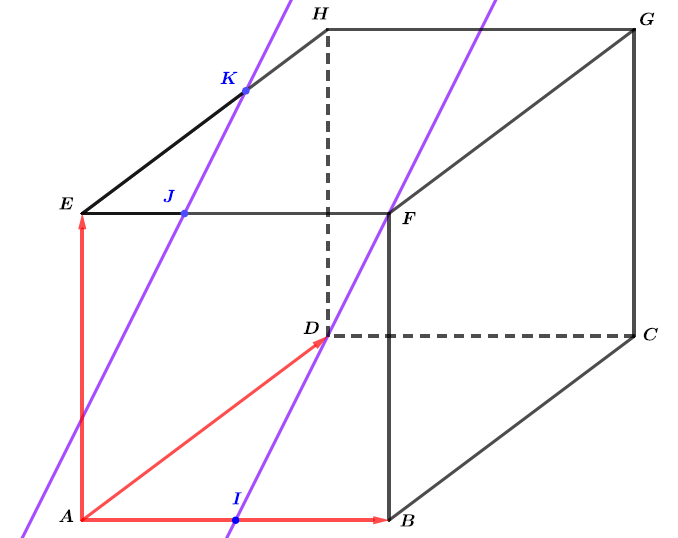
On connaît les coordonnées de et .
Si les vecteurs et colinéaires alors les et seront bien parallèles
On sait les coordonnées des points suivants ; ; et
On calcule les vecteurs et
Existe-t-il un réel tel que ?
On obtient le système suivant
Ainsi
Il en résulte que .
Les vecteurs et sont colinéaires alors les et sont bien parallèles.
