La géométrie dans l'espace et produit scalaire
Exercices types : ème partie - Exercice 3
35 min
55
Soit le cube représenté ci-dessous. On considère :
et les milieux respectifs des segments et le centre de la face , c’est-à-dire l’intersection des diagonales et le milieu du segment . 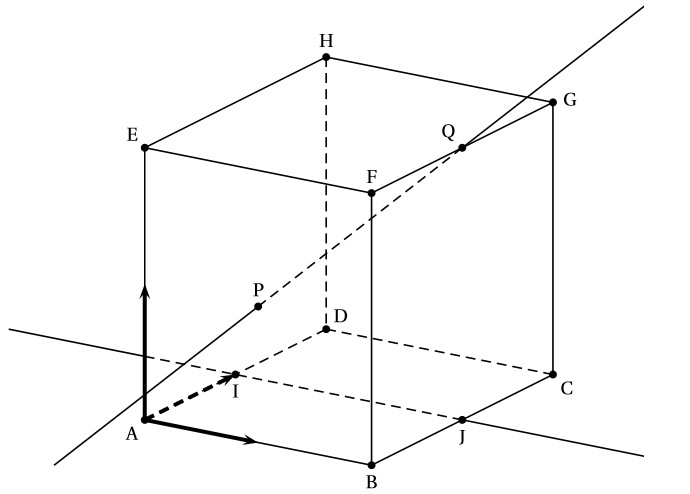

Question 1
On se place dans le repère orthonormé .
Dans tout l’exercice, on pourra utiliser les coordonnées des points de la figure.
On admet qu’une représentation paramétrique de la droite est : où
Dans tout l’exercice, on pourra utiliser les coordonnées des points de la figure.
On admet qu’une représentation paramétrique de la droite est : où
Donner les coordonnées de tous les points de la figure.
Correction
On considère le repère . Si l'on veut déterminer les coordonnées par exemple d'un point il faut l'exprimer le point avec l'origine du repère en fonction des vecteurs du repère donné. Dans notre exemple, si alors les coordonnées de sont

est l'origine du repère ainsi
, , , , , , , , et
Question 2
Déterminer une représentation paramétrique de la droite .
Correction
- On commence par calculer le vecteur qui est un vecteur directeur de la droite . Ensuite soit un point de cordonnées qui appartient à la droite . Cela signifie que les points et sont alignés donc les vecteurs et sont colinéaires.
Il existe alors un réel tel que . On aura ainsi la droite .
Cela donne :
puis
Les points , et sont alignés, donc les vecteurs et sont colinéaires.
Cela se traduit par :
, ce qui donne où
Finalement l'équation paramétrique de est :
où
Question 3
Soient un nombre réel et le point de la droite de paramètre .
On admet qu’il existe un unique point appartenant à la droite tel que soit orthogonale à .
On admet qu’il existe un unique point appartenant à la droite tel que soit orthogonale à .
Démontrer que les coordonnées de ce point sont .
Correction
D'après l'énoncé, on admet qu’une représentation paramétrique de la droite est : où
Le point appartenant à la droite donc les coordonnées du point sont de la forme :
Les droites et sont orthogonales, il en résulte donc que les vecteurs et sont orthogonaux. Cela signifie donc que le produit scalaire est nul. Autrement dit :
Il faut maintenant calculer les vecteurs et .
D'où :
puis
équivaut successivement à :
Les coordonnées du point sont de la forme : c'est à dire
Le point appartenant à la droite donc les coordonnées du point sont de la forme :
Les droites et sont orthogonales, il en résulte donc que les vecteurs et sont orthogonaux. Cela signifie donc que le produit scalaire est nul. Autrement dit :
Il faut maintenant calculer les vecteurs et .
D'où :
puis
équivaut successivement à :
Les coordonnées du point sont de la forme : c'est à dire
Question 4
En déduire que .
Correction
Nous connaissons les coordonnées de et de . Ainsi :
équivaut successivement à :
car
équivaut successivement à :
car
Question 5
Vérifier que est une équation cartésienne du plan .
Correction
Nous savons d'après la question que , et
 On vérifie facilement que les points , et ne sont pas alignés, ils forment donc bien le plan .
On vérifie facilement que les points , et ne sont pas alignés, ils forment donc bien le plan .
Il faut que les coordonnées des trois points vérifient l'équation cartésienne du plan .
Vérifions si le point appartient au plan.
donc le point appartient au plan.
Vérifions si le point appartient au plan.
donc le point appartient au plan.
Vérifions si le point appartient au plan.
donc le point appartient au plan.
Donc l'équation cartésienne du plan est bien .

Il faut que les coordonnées des trois points vérifient l'équation cartésienne du plan .
Vérifions si le point appartient au plan.
donc le point appartient au plan.
Vérifions si le point appartient au plan.
donc le point appartient au plan.
Vérifions si le point appartient au plan.
donc le point appartient au plan.
Donc l'équation cartésienne du plan est bien .