La géométrie dans l'espace et produit scalaire
Exercices types : ème partie - Exercice 2
35 min
70
On considère un cube .
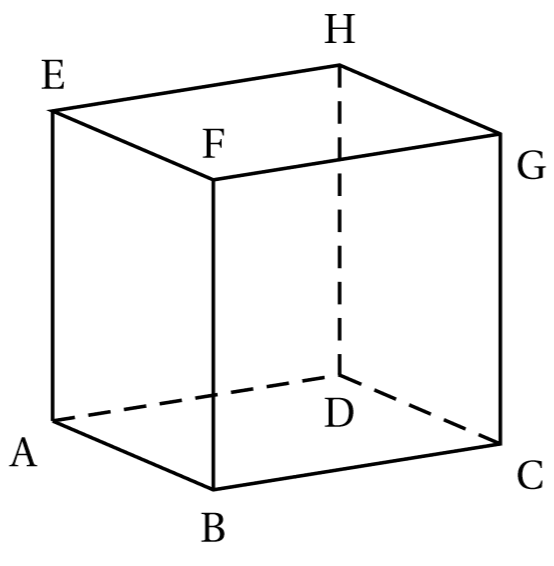

Question 1
Simplifier le vecteur .
Correction
Comme est un cube alors
Ainsi :
. Finalement :
Ainsi :
. Finalement :
d'après la relation de Chasles.
Question 2
En déduire que
Correction
Comme alors :
Dans le carré , les diagonales et sont perpendiculaires. Ainsi : La droite est perpendiculaire au plan donc les vecteurs et sont orthogonaux; il en résulte que :
Finalement :
Finalement :
Question 3
On admet que
Démontrer que la droite est orthogonale au plan .
Correction
Question 4
L’espace est muni du repère orthonormé .
Démontrer qu’une équation cartésienne du plan est .
Correction
On considère le repère . Si l'on veut déterminer les coordonnées par exemple d'un point il faut l'exprimer le point avec l'origine du repère en fonction des vecteurs du repère donné. Dans notre exemple, si alors les coordonnées de sont
Nous travaillons avec le repère orthonormé Nous allons décomposer le vecteur en fonction des vecteurs , et .
D'après la question , on sait que :
et donc que :
Enfin :
Les cordonnées du point sont alors :
D’après la question , la droite est orthogonale au plan donc le vecteur est un vecteur normal au plan .
Il en résulte que le plan s'écrit : . Or le point appartient au plan . Les coordonnées du point dans le repère sont
Il en résulte que : donne .
L'équation cartésienne du plan est bien :
Question 5
Déterminer les coordonnées du point d’intersection de la droite et du plan .
Correction
- Soit une droite définie par un point et un vecteur directeur . La droite admet donc un système d’équations paramètriques, appelé représentation paramétrique, de la forme : où
Pour déterminer les coordonnées du point d’intersection de la droite et du plan , il nous faut résoudre le système suivant:
où
Les coordonnées du pont sont
Question 6
On admet que l’aire ,en unité d’aire, du triangle est égale à .
Calculer le volume de la pyramide .
Correction
Le volume de la pyramide est donné par la formule
Ici l'aire de la base est qui vaut .
De plus, la hauteur de la pyramide est issue de . D’après les questions précédentes, cette hauteur est la longueur .
Finalement :
D'où :
Ici l'aire de la base est qui vaut .
De plus, la hauteur de la pyramide est issue de . D’après les questions précédentes, cette hauteur est la longueur .
Finalement :
D'où :