La géométrie dans l'espace et produit scalaire
Exercice 4 déja utilisé expert - Exercice 1
1 min
0
Cet exercice est un questionnaire à choix multiples.
Pour chacune de ces questions, une seule des réponses proposées est exacte.
On demande bien sûr de justifier.
Pour chacune de ces questions, une seule des réponses proposées est exacte.
On demande bien sûr de justifier.
Question 1
La figure ci-dessous représente un cube d'arête .
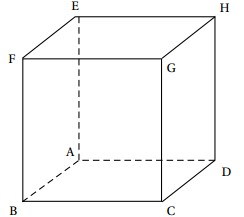 Le produit scalaire est égale à :
Le produit scalaire est égale à :
-
-
-
-

Correction
La bonne réponse est a.
équivaut successivement à
. Or .
Ainsi,
.
Or est perpendiculaire à mais aussi à .
Il vient alors que :
équivaut successivement à
. Or .
Ainsi,
.
Or est perpendiculaire à mais aussi à .
Il vient alors que :
Question 2
est une pyramide à base carré et à sommet dont toutes les arêtes ont la même mesure .
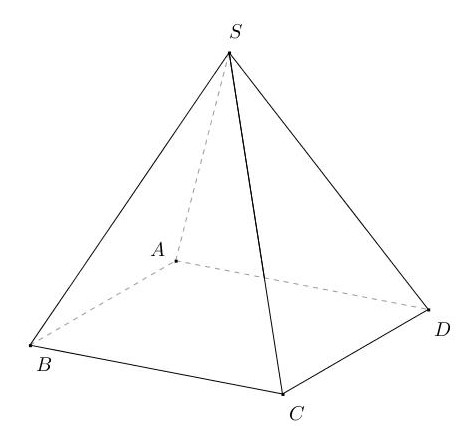
Le produit scalaire est égale à :
-
-
-
-

Le produit scalaire est égale à :
Correction
La bonne réponse est c.
car est équilatéral.
Question 3
Soit la droite de représentation paramétrique où et le plan d'équation cartésienne .
Alors :
- et sont sécants
- et sont orthogonaux
- est strictement parallèle à
- est incluse dans
Alors :
- et sont sécants
- et sont orthogonaux
- est strictement parallèle à
- est incluse dans
Correction
La bonne réponse est c.
Soient un vecteur normal du plan et un vecteur directeur de .
On vérifie aisément que les vecteurs et ne sont pas colinéaires, donc le plan et la droite ne sont pas orthogonaux.
De plus .
Cela signifie que le plan et la droite sont parallèles.
Mais on remarque que dans les choix des réponses proposées, le plan et la droite sont confondues.
Vérifions alors cette éventualité.
On cherche à démontrer si le plan et la droite ont des points en communs.
Si tel est le cas alors le plan et la droite sont confondues car on sait déjà qu'ils sont parallèles.
où .
On remplace la valeur de , et dans le plan
équivaut successivement à
Ainsi
La première ligne est une équation impossible.
Cela signifie que le plan et la droite n'ont aucun point d'intersection, le plan et la droite sont donc strictement parallèles.
Soient un vecteur normal du plan et un vecteur directeur de .
On vérifie aisément que les vecteurs et ne sont pas colinéaires, donc le plan et la droite ne sont pas orthogonaux.
De plus .
Cela signifie que le plan et la droite sont parallèles.
Mais on remarque que dans les choix des réponses proposées, le plan et la droite sont confondues.
Vérifions alors cette éventualité.
On cherche à démontrer si le plan et la droite ont des points en communs.
Si tel est le cas alors le plan et la droite sont confondues car on sait déjà qu'ils sont parallèles.
où .
On remplace la valeur de , et dans le plan
équivaut successivement à
Ainsi
La première ligne est une équation impossible.
Cela signifie que le plan et la droite n'ont aucun point d'intersection, le plan et la droite sont donc strictement parallèles.
Question 4
Soient , , et quatre points de l'espace.
Alors est l'équation cartésienne du plan :
-
-
-
-
Alors est l'équation cartésienne du plan :
Correction
La bonne réponse est c.
Il suffit de vérifier quels sont les points qui appartiennent à l'équation cartésienne donné.
Le point appartient au plan car
Le point appartient au plan car
Le point appartient au plan car
L'équation cartésienne est celle du plan .
Il suffit de vérifier quels sont les points qui appartiennent à l'équation cartésienne donné.
Le point appartient au plan car
Le point appartient au plan car
Le point appartient au plan car
L'équation cartésienne est celle du plan .
Question 5
On considère deux droites et ayant pour représentations paramétriques :
où et où
Les droites et sont :
- Non coplanaires
- Strictement parallèles
- Confondues
- Orthogonales
où et où
Les droites et sont :
- Non coplanaires
- Strictement parallèles
- Confondues
- Orthogonales
Correction
La bonne réponse est a.
On note et respectivement les vecteurs directeurs des droites et .
On vérifie facilement que les vecteurs et ne sont pas colinéaires.
Il en résulte que les droites et ne sont pas parallèles.
De plus, .
Il en résulte que les droites et ne sont pas orthogonales.
Il nous reste à voir si les droites sont sécantes.
Il faut résoudre le système constitué des deux écritures paramétriques des droites et , et déterminons les valeurs de et .
avec la troisième ligne on exprime en fonction de .
on remplace ensuite dans la 1ère équation et dans la 2ème pour déterminer la valeur de .
équivaut successivement à
Ici la 2ème ligne est une égalité fausse.
Les droites et ne sont donc pas sécantes.
On peut conclure alors que les droites et ne sont pas coplanaires.
On note et respectivement les vecteurs directeurs des droites et .
On vérifie facilement que les vecteurs et ne sont pas colinéaires.
Il en résulte que les droites et ne sont pas parallèles.
De plus, .
Il en résulte que les droites et ne sont pas orthogonales.
Il nous reste à voir si les droites sont sécantes.
Il faut résoudre le système constitué des deux écritures paramétriques des droites et , et déterminons les valeurs de et .
avec la troisième ligne on exprime en fonction de .
on remplace ensuite dans la 1ère équation et dans la 2ème pour déterminer la valeur de .
équivaut successivement à
Ici la 2ème ligne est une égalité fausse.
Les droites et ne sont donc pas sécantes.
On peut conclure alors que les droites et ne sont pas coplanaires.
Question 6
Dans l'espace rapporté à un repère , est l'équation :
- De la droite de vecteur directeur passant par le point
- De la droite de vecteur directeur passant par le point
- Du plan de vecteur normal passant par le point
- Du plan de vecteur normal passant par le point
- De la droite de vecteur directeur passant par le point
- De la droite de vecteur directeur passant par le point
- Du plan de vecteur normal passant par le point
- Du plan de vecteur normal passant par le point
Correction
La bonne réponse est d.
Ne vous méprenez pas ressemble à l'écriture d'une droite mais ici nous sommes dans l'espace.
Ainsi s'écrit .
On peut aussi écrire (on a multiplié le membre de gauche et celui de droite par )
On reconnaît donc l'écriture cartésienne d'un plan donc le vecteur normal est .
De plus le point appartient au plan car
Ne vous méprenez pas ressemble à l'écriture d'une droite mais ici nous sommes dans l'espace.
Ainsi s'écrit .
On peut aussi écrire (on a multiplié le membre de gauche et celui de droite par )
On reconnaît donc l'écriture cartésienne d'un plan donc le vecteur normal est .
De plus le point appartient au plan car
Question 7
Soit un repère orthonormé .
Soient les points , , et où .
La valeur de pour que , , et soient coplanaires est :
-
-
-
-
Soient les points , , et où .
La valeur de pour que , , et soient coplanaires est :
Correction
La bonne réponse est c.
, et
Nous allons résoudre dans un premier temps le système composée de la ligne 1 et de la ligne 3 afin de déterminer les valeurs de et .
Il vient alors que :
On utilise la méthode par combinaison.
On multiplie la ligne 1 par .
Il vient alors que :
On additionne maintenant les deux lignes et on pourra ainsi déterminer la valeur de .
on obtient et on remplace dans la première ligne et on obtient : donc .
On a montré que et .
On remplace ces valeurs dans .
Il vient alors que :
Les points , , et sont donc coplanaires si .
les points , , et sont coplanaires s'il existe deux réels et tels que :
Calculons maintenant les vecteurs , et ., et
Nous allons résoudre dans un premier temps le système composée de la ligne 1 et de la ligne 3 afin de déterminer les valeurs de et .
Il vient alors que :
On utilise la méthode par combinaison.
On multiplie la ligne 1 par .
Il vient alors que :
On additionne maintenant les deux lignes et on pourra ainsi déterminer la valeur de .
on obtient et on remplace dans la première ligne et on obtient : donc .
On a montré que et .
On remplace ces valeurs dans .
Il vient alors que :
Les points , , et sont donc coplanaires si .
Question 8
On considère les plans respectifs et .
Les plans et sont sécants suivant la droite :
- où
- où
- où
- où
Les plans et sont sécants suivant la droite :
- où
- où
- où
- où
Correction
La bonne réponse est b.
Les plans et sont sécants suivant une droite : cela signifie que la droite est confondue avec le plan et confondue également avec le plan .
Vérifions si la droite est confondue avec le plan .
Cela revient à chercher les points d'intersections entre la droite et le plan.
où .
On remplace la valeur de , et dans le plan
équivaut successivement à
Ainsi
Or l'équation est une équation toujours vraie.
Cela signifie que le plan et la droite sont confondus.
Effectuons le même raisonnement pour savoir si la droite est confondue avec le plan .
Cela revient à chercher les points d'intersections entre la droite et le plan.
où .
On remplace la valeur de , et dans le plan
équivaut successivement à
Ainsi
Or l'équation est une équation toujours vraie.
Cela signifie que le plan et la droite sont confondus.
Les plans et sont sécants suivant la droite où
Les plans et sont sécants suivant une droite : cela signifie que la droite est confondue avec le plan et confondue également avec le plan .
Vérifions si la droite est confondue avec le plan .
Cela revient à chercher les points d'intersections entre la droite et le plan.
où .
On remplace la valeur de , et dans le plan
équivaut successivement à
Ainsi
Or l'équation est une équation toujours vraie.
Cela signifie que le plan et la droite sont confondus.
Effectuons le même raisonnement pour savoir si la droite est confondue avec le plan .
Cela revient à chercher les points d'intersections entre la droite et le plan.
où .
On remplace la valeur de , et dans le plan
équivaut successivement à
Ainsi
Or l'équation est une équation toujours vraie.
Cela signifie que le plan et la droite sont confondus.
Les plans et sont sécants suivant la droite où
Question 9
Soit un repère orthonormé .
Soient les points , et .
Le triangle est :
- Rectangle et non isocèle
- Isocèle et non rectangle
- Rectangle et isocèle
- Equilatéral
Soient les points , et .
Le triangle est :
- Rectangle et non isocèle
- Isocèle et non rectangle
- Rectangle et isocèle
- Equilatéral
Correction
La bonne réponse est b.
On calcule les trois côtés du triangle .
Le triangle est isocèle non rectangle.
On calcule les trois côtés du triangle .
Le triangle est isocèle non rectangle.
Question 10
La figure ci-dessous représente un cube .
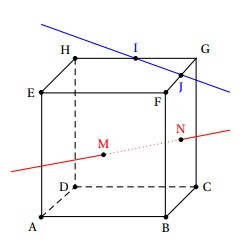
Les points et sont les milieux respectifs des arêtes et .
Les points et sont les centres respectifs des faces et .
Les droites et sont :
- Perpendiculaires
- Sécantes, non perpendiculaires
- Orthogonales
- Parallèles

Les points et sont les milieux respectifs des arêtes et .
Les points et sont les centres respectifs des faces et .
Les droites et sont :
- Perpendiculaires
- Sécantes, non perpendiculaires
- Orthogonales
- Parallèles
Correction
La bonne réponse est c.
Choisissons le repère .
En utilisant la figure, on a :
Pour le point :
.
On exprime maintenant à l'aide des vecteurs du repère .
Il vient alors :
.
Ainsi les coordonnées de sont
Pour le point :
.
On exprime maintenant à l'aide des vecteurs du repère .
Il vient alors :
.
Ainsi les coordonnées de sont
Pour le point :
est le centre de la face .
Les coordonnées de sont car est l'origine du repère.
Les coordonnées de sont car .
Comme est le milieu de alors
Pour le point on effectue le même raisonnement qu'avec le point .
On donne directement les coordonnées de qui sont .
On connait maintenant les coordonnées des points , , et .
On calcule les coordonnées des vecteurs et .
Il vient alors que :
et .
Or .
Les vecteurs et sont orthogonaux donc les droites et sont orthogonales.
On considère le repère
Si l'on veut déterminer les coordonnées par exemple d'un point il faut l'exprimer le point avec l'origine du repère en fonction des vecteurs du repère donné.
Dans notre exemple, si alors les coordonnées de sont
Si l'on veut déterminer les coordonnées par exemple d'un point il faut l'exprimer le point avec l'origine du repère en fonction des vecteurs du repère donné.
Dans notre exemple, si alors les coordonnées de sont
Choisissons le repère .
En utilisant la figure, on a :
Pour le point :
.
On exprime maintenant à l'aide des vecteurs du repère .
Il vient alors :
.
Ainsi les coordonnées de sont
Pour le point :
.
On exprime maintenant à l'aide des vecteurs du repère .
Il vient alors :
.
Ainsi les coordonnées de sont
Pour le point :
est le centre de la face .
Les coordonnées de sont car est l'origine du repère.
Les coordonnées de sont car .
Comme est le milieu de alors
Pour le point on effectue le même raisonnement qu'avec le point .
On donne directement les coordonnées de qui sont .
On connait maintenant les coordonnées des points , , et .
On calcule les coordonnées des vecteurs et .
Il vient alors que :
et .
Or .
Les vecteurs et sont orthogonaux donc les droites et sont orthogonales.
Question 11
Soit le plan d'équation paramétrique où et
Soit le plan d'équation cartésienne
Les plans et sont :
- Strictement parallèles
- Confondus
- Sécants
- Orthogonaux
Soit le plan d'équation cartésienne
Les plans et sont :
- Strictement parallèles
- Confondus
- Sécants
- Orthogonaux
Correction
La bonne réponse est a.
A l'aide de l'écriture paramétrique de on peut déterminer deux vecteurs directeurs que l'on note et .
De plus le point de coordonnées appartient au plan .
Avec l'écriture cartésienne de , on peut déterminer un vecteur normal de que l'on note .
On remarque également que :
Nous avons un vecteur normal de orthogonal à deux vecteurs non colinéaires du plan .
Cela signifie que les plans et sont parallèles.
Vérifions s'ils sont confondus.
Pour cela, nous savons que le point de coordonnées appartient au plan .
En est-il de même pour le plan ?
Il vient alors donc le point n'appartient pas au plan .
Les plans et sont strictement parallèles.
A l'aide de l'écriture paramétrique de on peut déterminer deux vecteurs directeurs que l'on note et .
De plus le point de coordonnées appartient au plan .
Avec l'écriture cartésienne de , on peut déterminer un vecteur normal de que l'on note .
On remarque également que :
Nous avons un vecteur normal de orthogonal à deux vecteurs non colinéaires du plan .
Cela signifie que les plans et sont parallèles.
Vérifions s'ils sont confondus.
Pour cela, nous savons que le point de coordonnées appartient au plan .
En est-il de même pour le plan ?
Il vient alors donc le point n'appartient pas au plan .
Les plans et sont strictement parallèles.
Question 12
Soit un repère orthonormé .
On considère les points , et et la droite d'équation où .
Le plan et la droite se coupent au point :
-
-
-
-
On considère les points , et et la droite d'équation où .
Le plan et la droite se coupent au point :
Correction
La bonne réponse est c.
Une équation du plan est .
Un point commun à ce plan et à la droite est obtenue en résolvant le système suivant :
où .
On remplace la valeur de , et dans le plan
Le point d'intersection au plan et à la droite est alors .
Une équation du plan est .
Un point commun à ce plan et à la droite est obtenue en résolvant le système suivant :
où .
On remplace la valeur de , et dans le plan
Le point d'intersection au plan et à la droite est alors .