La fonction logarithme
Exercice 1 DEJA UTILISE EN MATHS SPECIALITE - Exercice 1
1 min
0
Pour chacune des propositions suivantes, dire si elle est vraie ou fausse en justifiant la réponse.
Question 1
Soit une fonction définie sur par .
Proposition : « » .
Proposition : « » .
Correction
La proposition est fausse.
équivaut successivement à :
Question 2
Soit une fonction définie sur par .
Proposition : « » .
Proposition : « » .
Correction
La proposition est fausse.
On reconnaît la forme : avec et .
Ainsi et .
est dérivable sur , il vient alors que :
On reconnaît la forme : avec et .
Ainsi et .
est dérivable sur , il vient alors que :
Question 3
Soit une fonction définie sur par .
Proposition : « la fonction définie sur par est une primitive de ».
Proposition : « la fonction définie sur par est une primitive de ».
Correction
La proposition est fausse.
est dérivable sur .
On va commencer par calculer la dérivée de que l'on note .
donc :
Maintenant calculons la dérivée de qui est de la forme dont la dérivée est avec et
Ainsi :
La fonction définie sur par est bien une primitive de .
Dans le cas où une primitive est donnée, il vous suffit de dériver et d'obtenir comme résultat .
Autrement dit, il faut que :
Soit définie sur par .Autrement dit, il faut que :
est dérivable sur .
On va commencer par calculer la dérivée de que l'on note .
donc :
Maintenant calculons la dérivée de qui est de la forme dont la dérivée est avec et
Ainsi :
La fonction définie sur par est bien une primitive de .
Question 4
Soit une fonction définie sur par .
Proposition : « La courbe représentative de la fonction admet 3 tangentes horizontales ».
Proposition : « La courbe représentative de la fonction admet 3 tangentes horizontales ».
Correction
La proposition est vraie.
Une tangente horizontale admet un coefficient directeur égale à 0.
Cela signifie qu'il faut résoudre l'équation
Calculons donc la dérivée de :
est dérivable sur .
Pour faciliter nos calculs on pose
On reconnaît la forme : avec et .
Ainsi et .
Ainsi :
Nous pouvons donc maintenant calculer la dérivée de .
.
On met tout au même dénominateur.
Résolvons maintenant :
et
Les solutions de l'équation sont donc , et .
La courbe représentative de la fonction admet tangentes horizontales aux points d'abscisse , et .
Une tangente horizontale admet un coefficient directeur égale à 0.
Cela signifie qu'il faut résoudre l'équation
Calculons donc la dérivée de :
est dérivable sur .
Pour faciliter nos calculs on pose
On reconnaît la forme : avec et .
Ainsi et .
Ainsi :
Nous pouvons donc maintenant calculer la dérivée de .
.
On met tout au même dénominateur.
Résolvons maintenant :
et
Les solutions de l'équation sont donc , et .
La courbe représentative de la fonction admet tangentes horizontales aux points d'abscisse , et .
Question 5
Soit une fonction définie sur par .
Proposition : « l'équation admet une unique solution sur l'intervalle ».
Proposition : « l'équation admet une unique solution sur l'intervalle ».
Correction
La proposition est vraie.
Etudions le signe de la dérivée de .
est dérivable sur .
Posons tout d'abord et calculons la dérivée de .
On reconnaît la forme : avec et .
Ainsi et .
Il en résulte que la dérivée de s'écrit :
Comme donc et est strictement croissante sur l'intervalle
Calculons et .
On dresse le tableau de variation de :
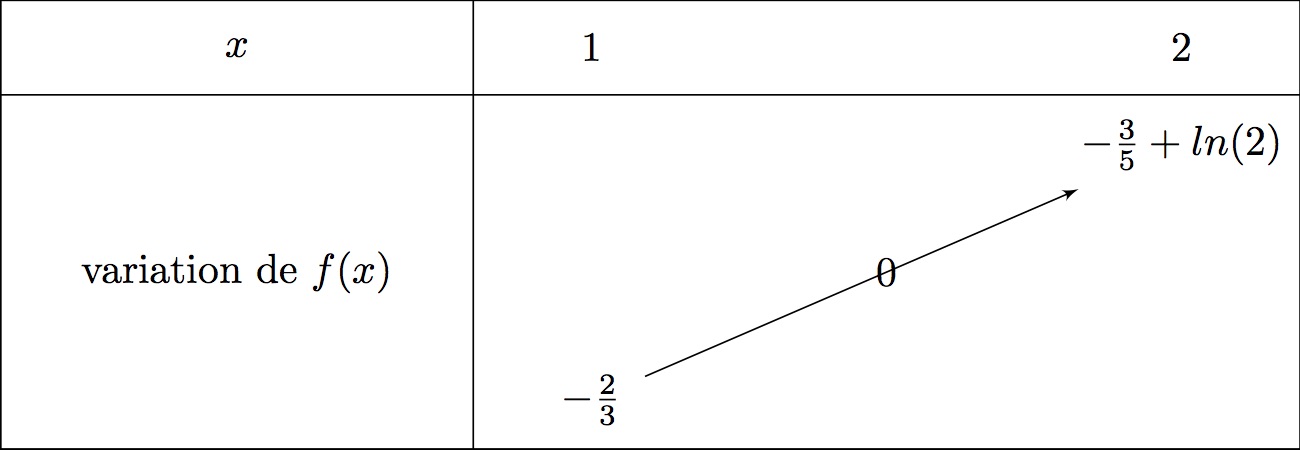 Sur , la fonction est continue et strictement croissante.
Sur , la fonction est continue et strictement croissante.
De plus, et .
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que .
Etudions le signe de la dérivée de .
est dérivable sur .
Posons tout d'abord et calculons la dérivée de .
On reconnaît la forme : avec et .
Ainsi et .
Il en résulte que la dérivée de s'écrit :
Comme donc et est strictement croissante sur l'intervalle
Calculons et .
On dresse le tableau de variation de :

De plus, et .
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que .
Question 6
Soient et deux fonctions définies sur par et .
Proposition : « La fonction est une primitive de ».
Proposition : « La fonction est une primitive de ».
Correction
La proposition est vraie.
Si alors la fonction est une primitive de .
est dérivable sur , ainsi où et .
Nous allons décomposer ainsi la dérivée afin de faciliter nos calculs.
D'une part : calcul de la dérivée de
On reconnaît la forme : avec et .
Ainsi et .
Ainsi :
D'autre part : calcul de la dérivée de
On reconnaît la forme avec et .
Ainsi et .
Ainsi :
Finalement :
Donc la fonction est une primitive de .
Si alors la fonction est une primitive de .
est dérivable sur , ainsi où et .
Nous allons décomposer ainsi la dérivée afin de faciliter nos calculs.
D'une part : calcul de la dérivée de
On reconnaît la forme : avec et .
Ainsi et .
Ainsi :
D'autre part : calcul de la dérivée de
On reconnaît la forme avec et .
Ainsi et .
Ainsi :
Finalement :
Donc la fonction est une primitive de .
Question 7
Soit une fonction définie et continue sur par.
Proposition : « ».
Proposition : « ».
Correction
La proposition est fausse.
Ainsi :
Finalement, une primitive de est alors
Il en résulte que :
Une primitive de la forme est de la forme
Soient donc Ainsi :
Finalement, une primitive de est alors
Il en résulte que :
Question 8
Soit une fonction définie sur par où et sont deux réels.
La courbe représentative de la fonction passe par le point et admet en ce point une tangente parallèle à la droite d'équation .
Proposition : « la fonction s'écrit ».
La courbe représentative de la fonction passe par le point et admet en ce point une tangente parallèle à la droite d'équation .
Proposition : « la fonction s'écrit ».
Correction
La proposition est vraie.
D'après l'énoncé, on en déduit deux informations
Tout d'abord, calculons la dérivée de .
une fonction dérivable sur , on a :
Maintenant exploitons les informations de l'énoncé.
équivaut successivement à :
équivaut successivement à :
Or
Ainsi :
D'après l'énoncé, on en déduit deux informations
- Le nombre désigne le coefficient directeur de la droite tangente à la courbe au point d'abscisse . Dans cet exercice la tangente au point d'abscisse 1 est parallèle à la droite d'équation donc.
Tout d'abord, calculons la dérivée de .
une fonction dérivable sur , on a :
Maintenant exploitons les informations de l'énoncé.
équivaut successivement à :
équivaut successivement à :
Or
Ainsi :
Question 9
Soit une fonction définie sur par .
Proposition : « et ».
Proposition : « et ».
Correction
La proposition est vraie.
Ici il s'agit de limite par composition.
peut également s'écrire
Commençons par calculer
Dans un premier temps : .
On pose
D'où : . F
Finalement, par composition :
Ensuite, calculons
Dans un premier temps :
par quotient .
On pose
D'où : .
Finalement, par composition :
Ici il s'agit de limite par composition.
peut également s'écrire
Commençons par calculer
Dans un premier temps : .
On pose
D'où : . F
Finalement, par composition :
Ensuite, calculons
Dans un premier temps :
par quotient .
On pose
D'où : .
Finalement, par composition :
Question 10
Soit l'inéquation .
Proposition : « Les solutions de cette inéquation sont les entiers naturels tels que ».
Proposition : « Les solutions de cette inéquation sont les entiers naturels tels que ».
Correction
La proposition est fausse.
équivaut successivement à :
, or d'où
On cherche la valeur de à la calculatrice et on arrondi à l'entier supérieur.
(à la calculatrice on obtient et on arrondi à l'entier supérieur)
Finalement :
équivaut successivement à :
, or d'où
On cherche la valeur de à la calculatrice et on arrondi à l'entier supérieur.
(à la calculatrice on obtient et on arrondi à l'entier supérieur)
Finalement :
Question 11
A l'aide de la représentation graphique ci-dessous de la fonction :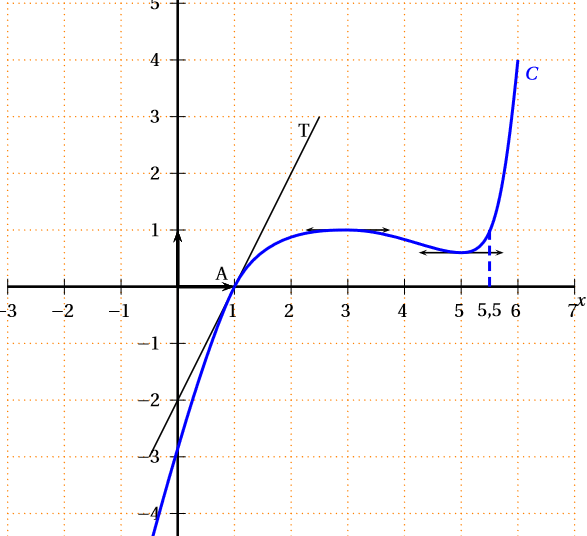 On a :
On a :

Correction
La proposition est vraie.
correspond au coefficient directeur de la tangente à la courbe au point d'abscisse . La tangente est horizontale. Cela signifie que le coefficient directeur est nul.
La tangente est horizontale. Cela signifie que le coefficient directeur est nul.
Ainsi :
correspond au coefficient directeur de la tangente à la courbe au point d'abscisse .

Ainsi :
Question 12
On considère la fonction définie sur par .
L'expression de la fonction dérivée de est alors : .
L'expression de la fonction dérivée de est alors : .
Correction
La proposition est vraie.
On reconnaît la forme : avec et .
Ainsi et . Pour faire la dérivée de , nous avons appliquer la formule .
. Nous allons maintenant factoriser par
car
Pour la dernière étape, nous allons multiplier par le premier facteur .
Cela nous permet donc d'écrire :
Ainsi et . Pour faire la dérivée de , nous avons appliquer la formule .
. Nous allons maintenant factoriser par
car
Pour la dernière étape, nous allons multiplier par le premier facteur .
Cela nous permet donc d'écrire :