Savoir résoudre des inéquations avec les exponentielles - Exercice 2

15 min

Question 1

Résoudre les inéquations suivantes sur

\mathbb{R}

.
A traiter uniquement si vous avez étudiez la fonction logarithme népérien .

$e^{x}-9 \ge 0$

Correction

$A=e^{\ln \left(A\right)}$ avec $A>0$

e^{x}-9 \ge 0

équivaut successivement à :

e^{x} \ge 9

e^{x}\ge e^{\ln \left(9\right)}

x\ge \ln 9

Donc :

S=\left[\ln 9;+\infty \right[

Question 2

$3-e^{-x} \le 0$

Correction

$A=e^{\ln \left(A\right)}$ avec $A>0$
$-\ln \left(A\right)=\ln \left(\frac{1}{A} \right)$

3-e^{-x} \le 0

équivaut successivement à :

-e^{-x} \le -3

e^{-x} \ge 3

e^{-x}\ge e^{\ln \left(3\right)}

-x\ge \ln 3

x\le-\ln 3

x\le \ln \left(\frac{1}{3} \right)

Donc :

S=\left]-\infty;\ln \left(\frac{1}{3} \right) \right]

Question 3

$e^{x}+2 \le 0$

Correction

On rappelle que pour tout réel

x

, on a :

e^{x}>0

donc

e^{x}+2>0

. Il en résulte que l'inéquation

e^{x}+2 \le 0

n'a aucun sens.
Il n'y a donc pas de solutions à cette inéquation.

Question 4

$2-e^{2-3x} \ge 0$

Correction

$A=e^{\ln \left(A\right)}$ avec $A>0$
$-\ln \left(A\right)=\ln \left(\frac{1}{A} \right)$

2-e^{2-3x} \ge 0

équivaut successivement à :

-e^{2-3x} \ge -2

e^{2-3x} \le 2

e^{2-3x}\le e^{\ln \left(2\right)}

2-3x\le \ln \left(2\right)

-3x\le \ln \left(2\right)-2

3x\ge -\ln \left(2\right)+2

x\ge \frac{-\ln \left(2\right)+2}{3}

Donc :

S=[\frac{-\ln \left(2\right)+2}{3};+\infty[

Question 5

$\left(e^{x} -4\right)\left(e^{x} +2\right)\le 0$

Correction

\left(e^{x} -4\right)\left(e^{x} +2\right)\le 0

. Pour résoudre cette inéquation, nous allons dresser un tableau de signe.
Pour tout réel

x

, on sait que

2>0

e^{x}>0

ou encore

e^{x}+2>0

.
De plus :

e^{x}-4\ge 0

équivaut successivement à :

e^{x}\ge 4

e^{x}\ge e^{\ln \left(4\right)}

x\ge \ln 4

. Cela signifie que

e^{x}-4

est positive ou nulle dès que

x\ge \ln 4

.
Nous traduisons cela dans un tableau de signe :

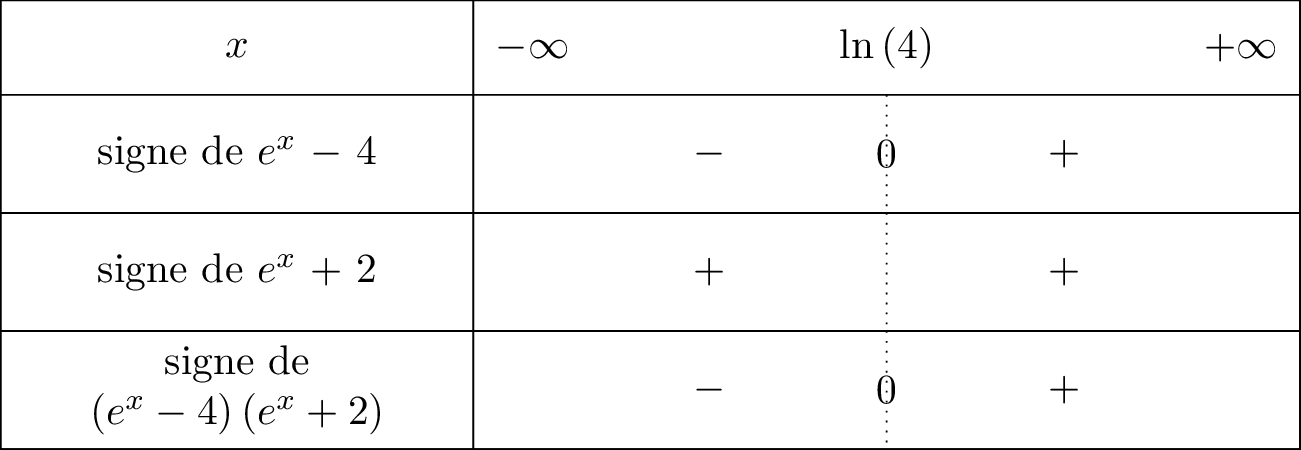Donc :

S=\left]-\infty ;\ln \left(4\right)\right]

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.

Savoir résoudre des inéquations avec les exponentielles - Exercice 2

ex−9≥0e^{x}-9 \ge 0ex−9≥0

3−e−x≤03-e^{-x} \le 03−e−x≤0

ex+2≤0e^{x}+2 \le 0ex+2≤0

2−e2−3x≥02-e^{2-3x} \ge 02−e2−3x≥0

(ex−4)(ex+2)≤0\left(e^{x} -4\right)\left(e^{x} +2\right)\le 0(ex−4)(ex+2)≤0

$e^{x}-9 \ge 0$

$3-e^{-x} \le 0$

$e^{x}+2 \le 0$

$2-e^{2-3x} \ge 0$

$\left(e^{x} -4\right)\left(e^{x} +2\right)\le 0$