La fonction exponentielle
Exercices types : 3ème partie - Exercice 2
50 min
75
Partie A : Etude d'une fonction auxiliaire.
Question 1
On considère la fonction définie sur par
Déterminer la limite de en .
Correction
Question 2
Déterminer la limite de en .
Correction
Pour relever cette indétermination, factorisons par .
Cela donne :
On a alors :
Finalement :
Question 3
Étudier le sens de variation de , puis dresser son tableau de variation.
Correction
est dérivable sur .
On a :
Résolvons l'inéquation :
équivaut successivement à :
Cela signifie que lorsque . Nous traduisons cela dans un tableau de variation, ainsi :
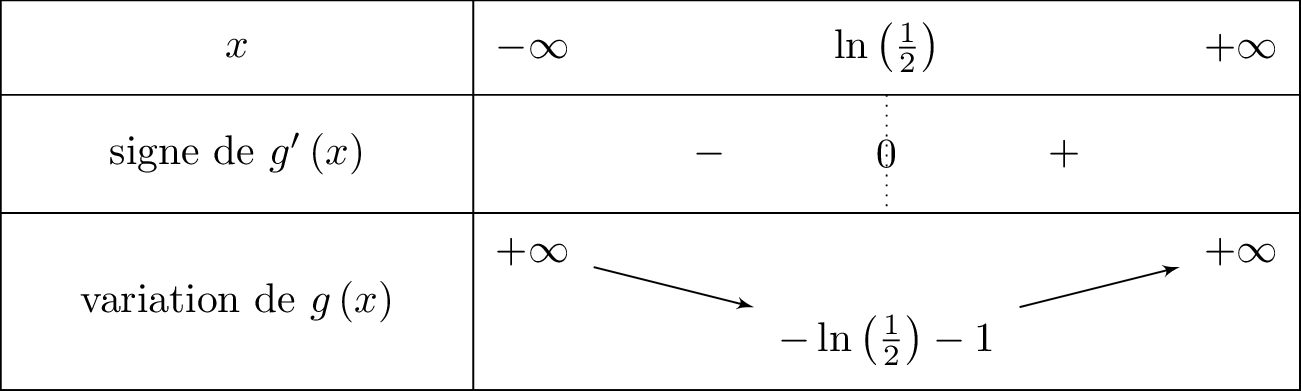 ainsi
ainsi
d'où
On a :
Résolvons l'inéquation :
équivaut successivement à :
Cela signifie que lorsque . Nous traduisons cela dans un tableau de variation, ainsi :

d'où
Question 4
On admet que l’équation a exactement deux solutions réelles.
Vérifier que est l’une de ces solutions.
Correction
donc est une de ces solutions.
Question 5
L’autre solution est appelée . Montrer que .
Correction
Nous allons faire apparaitre les zéros dans le tableau de variation. On a donc :
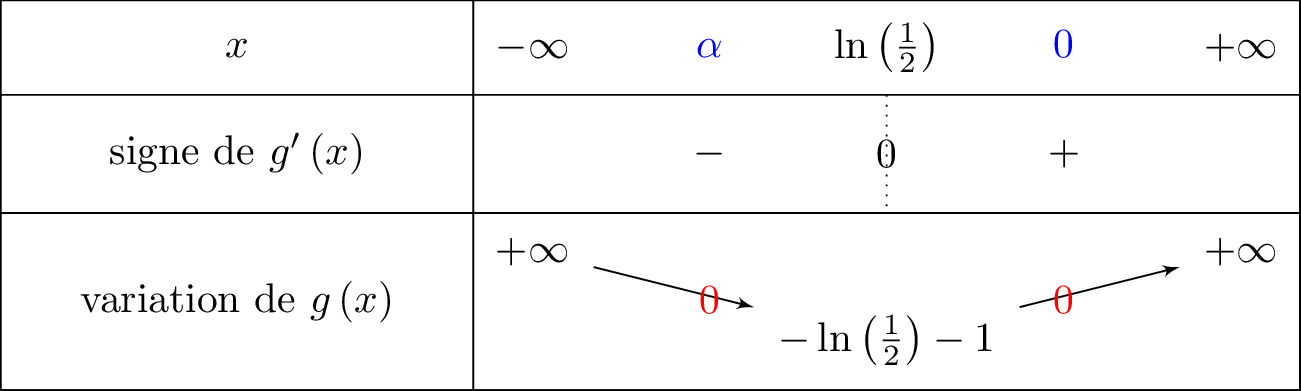 Sur , la fonction est continue et strictement décroissante.
Sur , la fonction est continue et strictement décroissante.
De plus, et .
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution appartenant à l'intervalle tel que .
Ainsi : .

De plus, et .
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution appartenant à l'intervalle tel que .
Ainsi : .
Question 6
Déterminer le signe de suivant les valeurs du réel .
Correction
Nous allons faire apparaitre les zéros dans le tableau de variation. On a donc :
 Il en résulte donc , d'après le tableau de variation, que :
Il en résulte donc , d'après le tableau de variation, que :
Sur l'intervalle , on a : Sur l'intervalle , on a : Sur l'intervalle , on a : Ainsi :


Question 7
Partie B : Etude de la fonction principale.
On considère la fonction définie sur par
On considère la fonction définie sur par
Déterminer la limite de en .
Correction
peut s'écrire
Question 8
Déterminer la limite de en . On mettra en facteur.
Correction
On a alors :
Finalement :
Question 9
Calculer et montrer que et ont le même signe.
Correction
Nous savons que
Ici on reconnaît la forme avec et .
On note
Ainsi : et , enfin
Il vient alors que :
. Nous allons maintenant factoriser par .
Pour tout réel , on sait que . Ainsi le signe de dépend de celui de .
Ici on reconnaît la forme avec et .
On note
Ainsi : et , enfin
Il vient alors que :
. Nous allons maintenant factoriser par .
Pour tout réel , on sait que . Ainsi le signe de dépend de celui de .
Question 10
Étudier le sens de variation de .
Correction
A la question , nous avons démontré que le signe de dépend de celui de .
A la question , nous avons déterminé le signe de .
 Nous pouvons donc dresser le tableau de variation de la fonction .
Nous pouvons donc dresser le tableau de variation de la fonction .
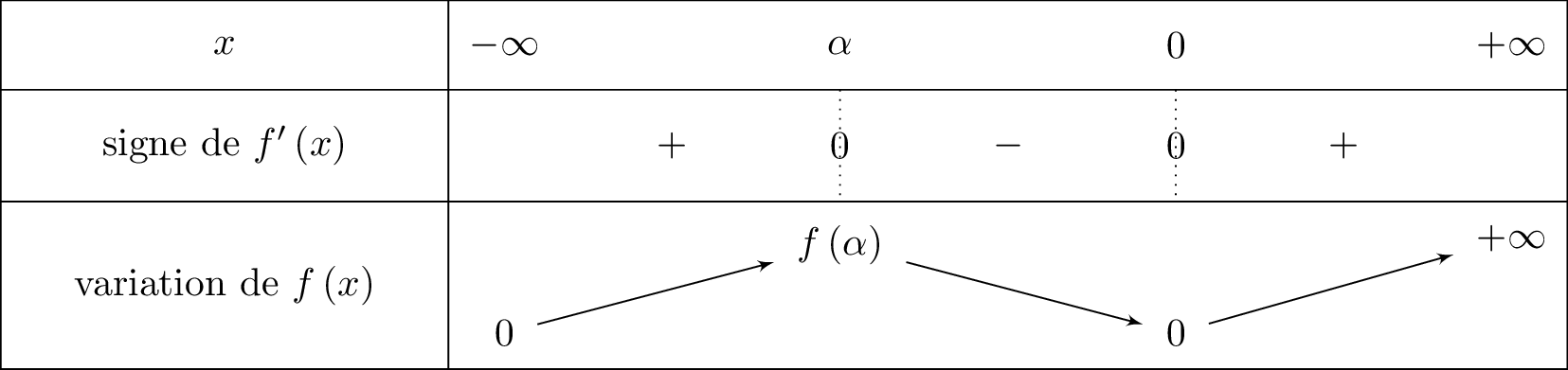
A la question , nous avons déterminé le signe de .

