La fonction exponentielle
Exercices types : 2ème partie - Exercice 2
50 min
75
Une chaîne, suspendue entre deux points d’accroche de même hauteur peut être modélisée par la représentation graphique d’une fonction définie sur par où est un paramètre réel strictement positif. On ne cherchera pas à étudier la fonction .
Question 1
On montre en sciences physiques que, pour que cette chaîne ait une tension minimale aux extrémités, il faut et il suffit que le réel soit une solution strictement positive de l’équation : .
Dans la suite de l'exercice , on définit sur la fonction par .
Dans la suite de l'exercice , on définit sur la fonction par .
Déterminer la fonction dérivée de la fonction .
Correction
est dérivable sur .
Ici on reconnaît la forme avec et .
On note . Ainsi et , enfin
Il vient alors que :
D'où :
Ici on reconnaît la forme avec et .
On note . Ainsi et , enfin
Il vient alors que :
D'où :
.
Question 2
Calculer et .
Correction
Nous rappelons que :
D'une part :
donc :
D'autre part :
:
Finalement :
D'une part :
donc :
D'autre part :
:
Finalement :
Question 3
On note la dérivée de la fonction .
Montrer que pour tout appartenant à on a : . Donner ensuite les variations de la fonction .
Correction
Nous rappelons que :
est dérivable sur .
Ici on reconnaît la forme avec et .
On note . Ainsi et , enfin
Il vient alors que :
Il en résulte donc que :
Pour tout appartenant à , on vérifie aisément que :
On dresse ci-dessous le tableau de variation de .
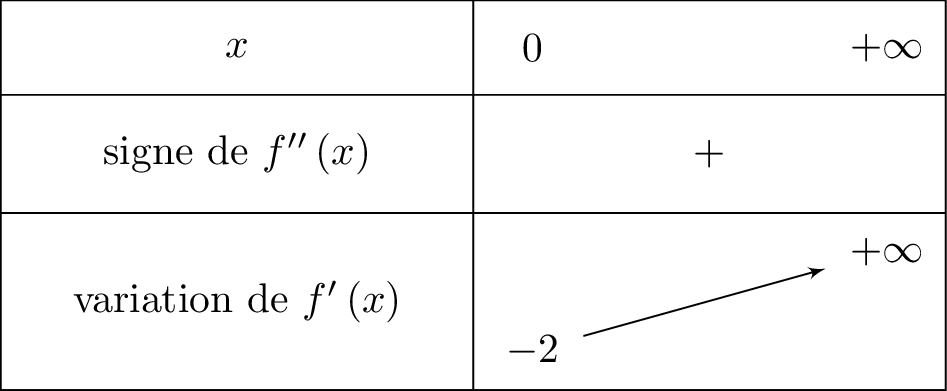
est dérivable sur .
Ici on reconnaît la forme avec et .
On note . Ainsi et , enfin
Il vient alors que :
Il en résulte donc que :
Pour tout appartenant à , on vérifie aisément que :
On dresse ci-dessous le tableau de variation de .
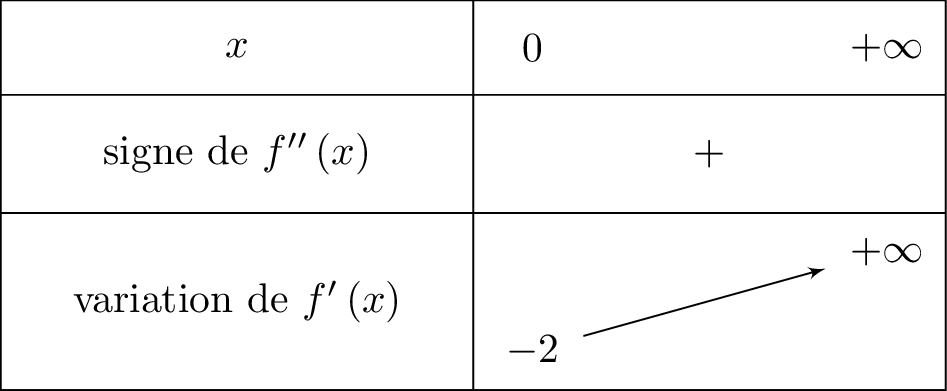
Question 4
Démontrez que l'équation admet une unique solution .
Donnez un encadrement de à près.
Donnez un encadrement de à près.
Correction
On reprend le tableau de variation fait à la question . On fera apparaître le zéro que l'on recherche.
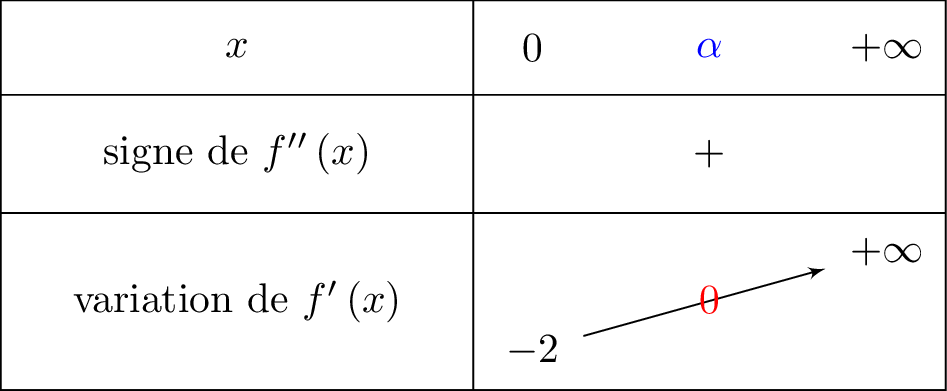 Sur , la fonction est continue et strictement croissante.
Sur , la fonction est continue et strictement croissante.
De plus, et . Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans l'intervalle tel que .
A la calculatrice, on vérifie que :
et . Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
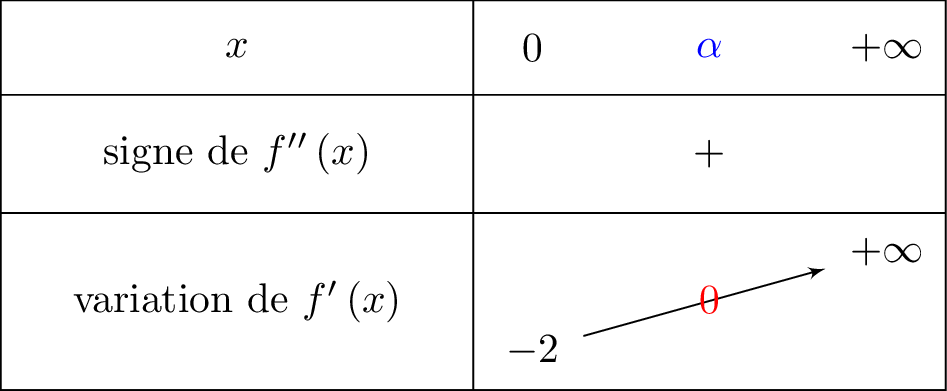
De plus, et . Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans l'intervalle tel que .
A la calculatrice, on vérifie que :
et . Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
Question 5
En déduire le signe de sur l'intervalle .
Correction
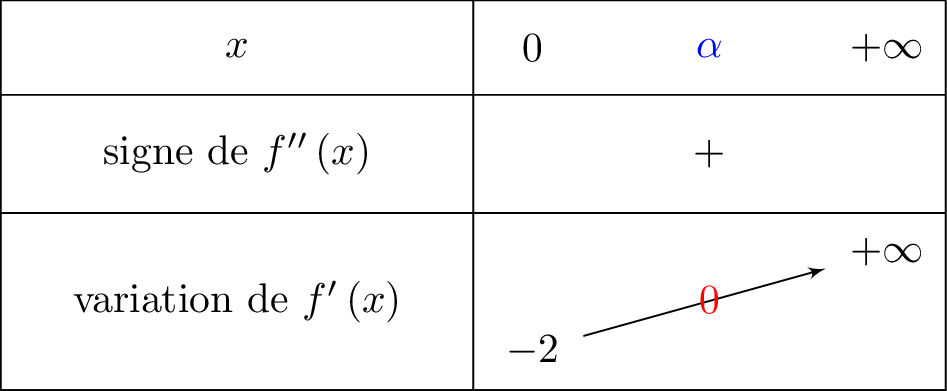
Donc pour tout et pour tout
On résume cela dans un tableau de signe :
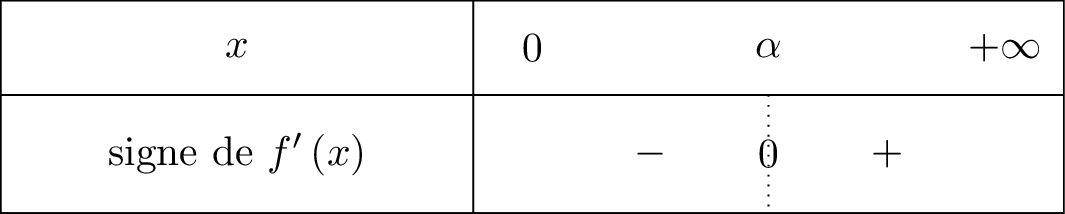
Question 6
Déterminer le sens de variation de la fonction sur l’intervalle puis montrer que est négatif pour tout réel appartenant à l’intervalle .
Correction
D'après la question , nous connaissons le signe de donc nous aurons les variations de .
Nous dressons le tableau de variation ci-dessous :
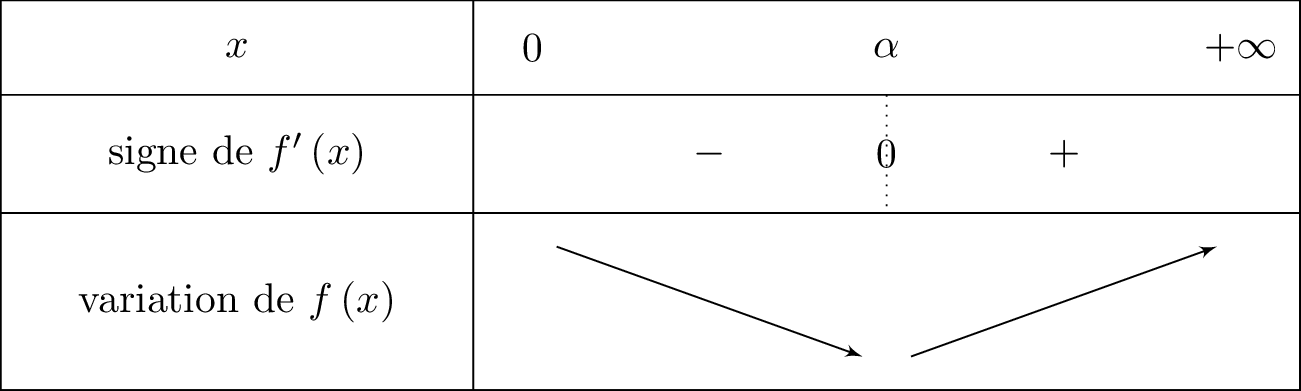 De plus :
De plus :
Comme la fonction est strictement décroissante sur et que , il en résulte donc que sur l'intervalle la fonction est strictement négative. Ainsi :
Pour tout réel on a :
Nous dressons le tableau de variation ci-dessous :

Comme la fonction est strictement décroissante sur et que , il en résulte donc que sur l'intervalle la fonction est strictement négative. Ainsi :
Question 7
Calculer .
Correction
ainsi .
Question 8
En déduire que sur l’intervalle , la fonction s’annule pour une unique valeur. Si l’on note cette valeur, déterminer à l’aide de la calculatrice la valeur de arrondie au centième.
Correction
Nous savons déjà, grâce à la question que pour tout réel on a :
Sur , la fonction est continue et strictement croissante.
De plus, et . D'après le théorème des valeurs intermédiaires, il existe une unique solution dans l'intervalle tel que .
De plus, et est strictement croissante sur donc l’équation n’a pas de solution dans l’intervalle . Comme pour tout réel , l’équation n’a pas de solution dans . On peut donc dire que l’équation admet une unique solution dans l’intervalle et que cette solution appartient à l’intervalle ; on l’appelle . En utilisant la calculatrice, on trouve .
Sur , la fonction est continue et strictement croissante.
De plus, et . D'après le théorème des valeurs intermédiaires, il existe une unique solution dans l'intervalle tel que .
De plus, et est strictement croissante sur donc l’équation n’a pas de solution dans l’intervalle . Comme pour tout réel , l’équation n’a pas de solution dans . On peut donc dire que l’équation admet une unique solution dans l’intervalle et que cette solution appartient à l’intervalle ; on l’appelle . En utilisant la calculatrice, on trouve .