La fonction exponentielle
Exercices types : 1ère partie - Exercice 5
30 min
45
Soit la fonction définie sur par
Question 1
Calculer les limites de en et .
Correction
calculons
D'où .
Finalement :
calculons
Nous allons développer l'expression de puis écrire que afin de relever l'indétermination.
Cela donne :
On rappelle ensuite que .
Ainsi donc
D'où .
Il existe donc une asymptote horizontale d'équation .
D'où .
Finalement :
calculons
Nous allons développer l'expression de puis écrire que afin de relever l'indétermination.
Cela donne :
On rappelle ensuite que .
Ainsi donc
D'où .
Il existe donc une asymptote horizontale d'équation .
Question 2
Etudier le sens de variation de puis dresser son tableau de variation.
Correction
Soit : .
est dérivable sur
Ici on reconnaît la forme avec et .
On note . Ainsi et , enfin
Il vient alors que :
Finalement :
Pour tout réel , on a .
Pour l'étude de , on va utiliser le discriminant.
Nous donnons directement les résultats car le discriminant n'a maintenant plus de secret pour nous.
, et .
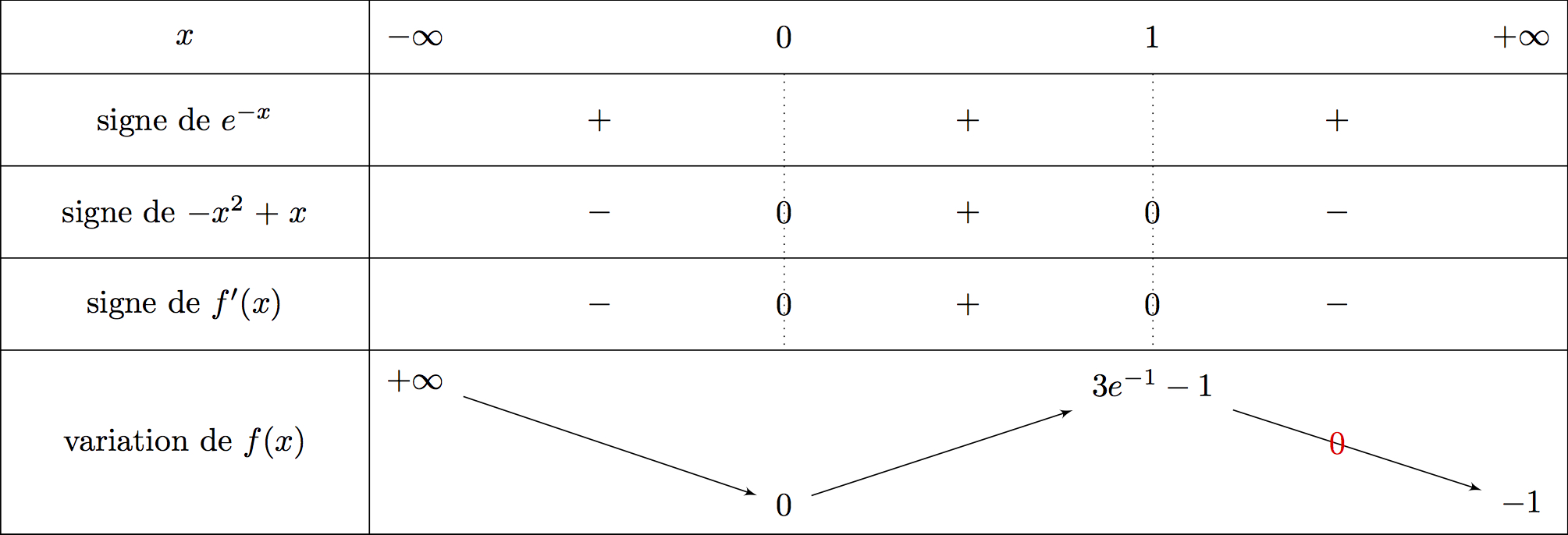
On en déduit le tableau de variation suivant :
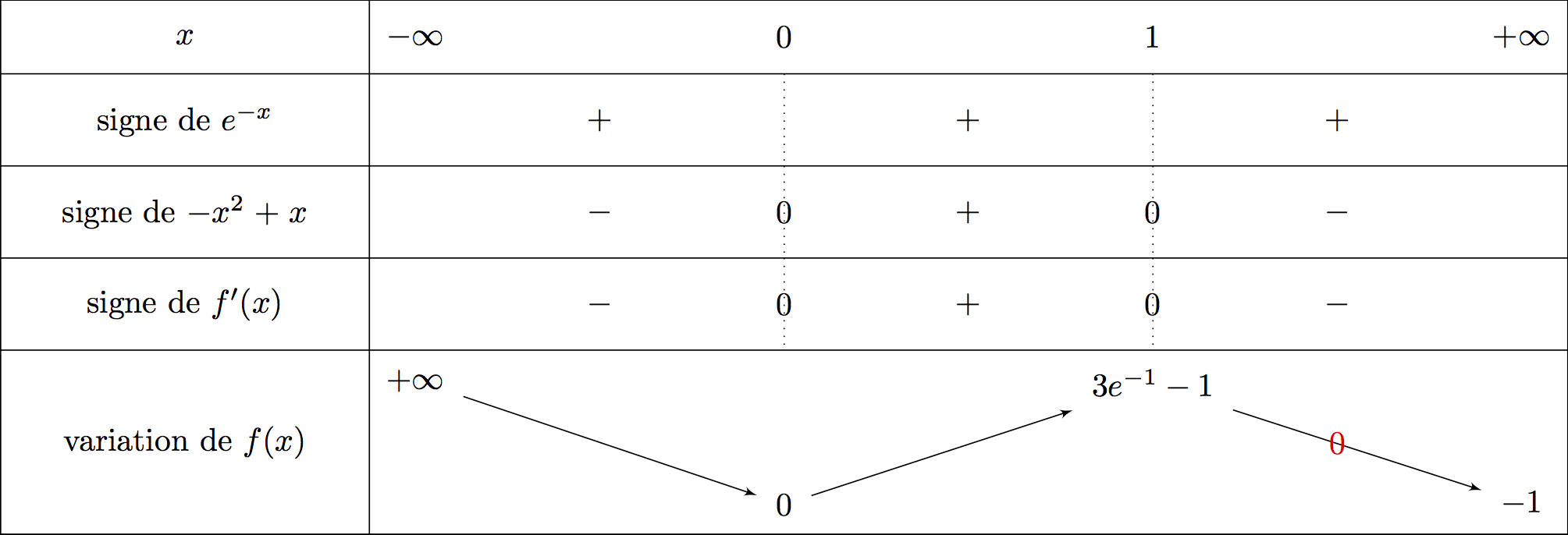
est dérivable sur
Ici on reconnaît la forme avec et .
On note . Ainsi et , enfin
Il vient alors que :
Finalement :
Pour tout réel , on a .
Pour l'étude de , on va utiliser le discriminant.
Nous donnons directement les résultats car le discriminant n'a maintenant plus de secret pour nous.
, et .
On en déduit le tableau de variation suivant :

Question 3
Démontrer que l'équation admet deux solutions dans , dont l'une dans l'intervalle , qui sera notée .
Correction
Ainsi l'équation admet une solution lorsque que .
Sur , la fonction est continue et strictement décroissante.
De plus, et . Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que .
Question 4
Déterminer un encadrement d'amplitude de .
Correction
A la calculatrice, on vérifie que :
et .
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que
et .
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que
Question 5
En déduire le signe de sur .
Correction
Sur , la fonction est continue et admet comme minimum.
Ainsi .
Sur , la fonction est continue et strictement décroissante et .
Donc pour tout et pour tout .
On résume cela dans un tableau de signe :

Ainsi .
Sur , la fonction est continue et strictement décroissante et .
Donc pour tout et pour tout .
On résume cela dans un tableau de signe :
