La fonction exponentielle
Exercices types : 1ère partie - Exercice 3
20 min
35
Soit la fonction définie sur par .
On note sa courbe représentative dans un repère orthogonal du plan.
On note sa courbe représentative dans un repère orthogonal du plan.
Question 1
Déterminer la limite de en .
Correction
Question 2
On admet que :
En déduire que admet une asymptote horizontale que l'on précisera.
Correction
Comme , il existe une asymptote horizontale d'équation .
Question 3
Etudier les variations de puis dresser son tableau de variation.
Correction
Soit
est dérivable sur
Ici on reconnait la forme avec et .
Ainsi et .
Il vient alors que :
. Nous allons maintenant factoriser par .
Pour tout réel , on a .
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera inférieur ou égale à .
On en déduit le tableau de variation suivant :
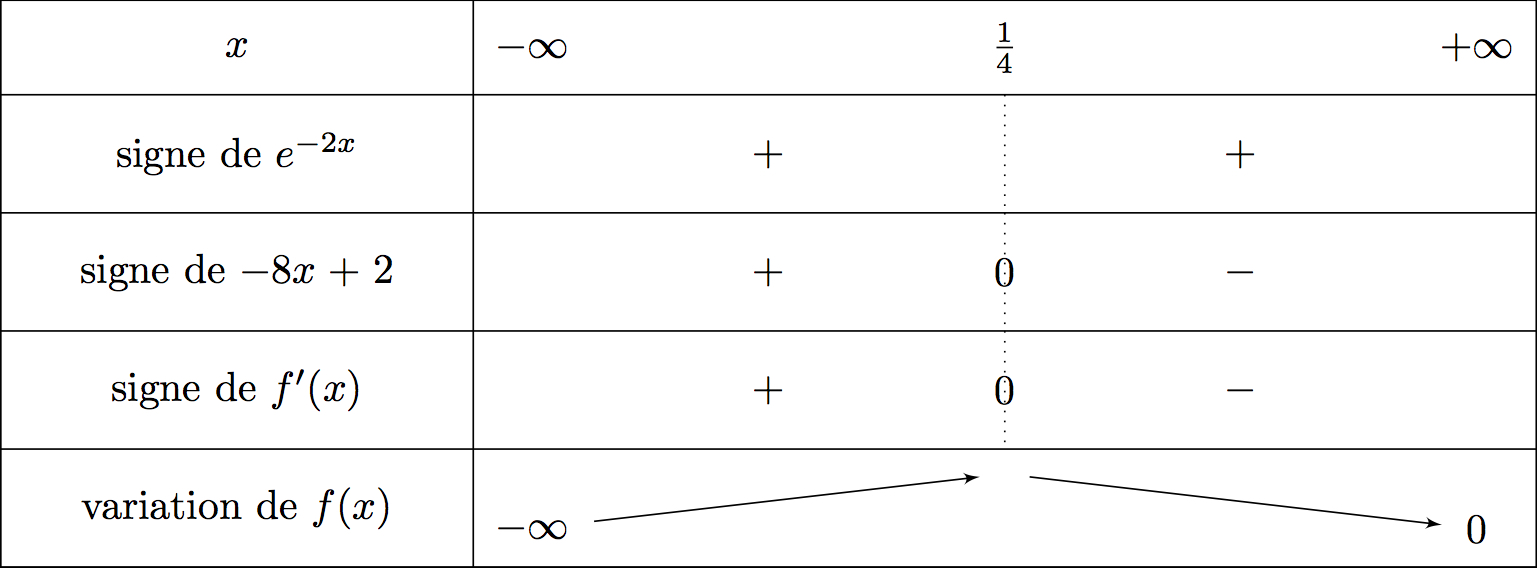
est dérivable sur
Ici on reconnait la forme avec et .
Ainsi et .
Il vient alors que :
. Nous allons maintenant factoriser par .
Pour tout réel , on a .
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera inférieur ou égale à .
On en déduit le tableau de variation suivant :

Question 4
Déterminer une équation de la tangente à au point d'abscisse .
Correction
La formule de l'équation de la tangente au point d'abscisse est donnée par :
Dans cette exercice, .
On a alors
Il en résulte que :
Dans cette exercice, .
On a alors
Il en résulte que :