La fonction exponentielle
Exercices types : 1ère partie - Exercice 2
35 min
55
Soit la fonction définie sur par .
Question 1
Calculer les limites de en et .
Correction
Question 2
Etudiez les variations de .
Correction
Soit
est dérivable sur
On a :
Pour tout réel , on a .
Il vient alors que :
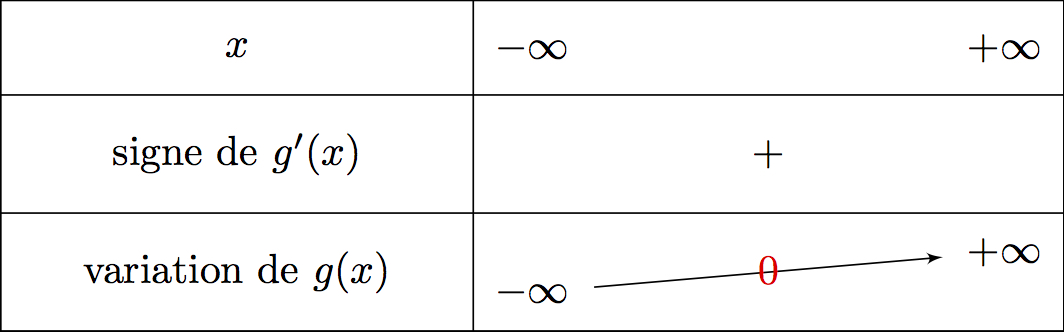
est dérivable sur
On a :
Pour tout réel , on a .
Il vient alors que :

Question 3
Démontrez que l'équation admet une unique solution .
Donnez un encadrement de à près.
Donnez un encadrement de à près.
Correction
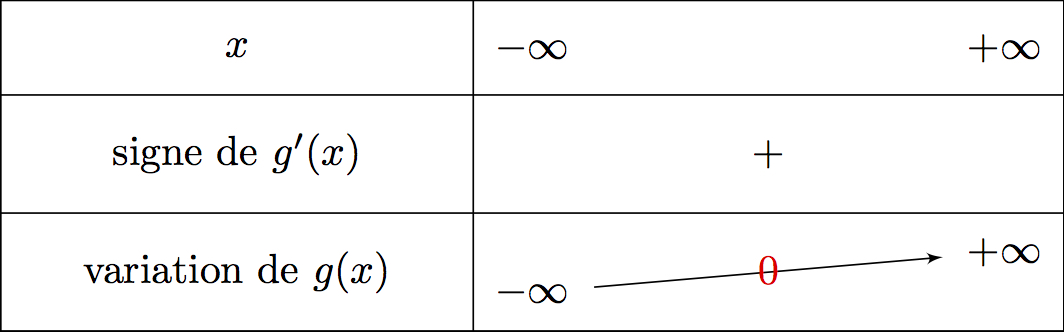
De plus, et . Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que .
A la calculatrice, on vérifie que :
et . Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
Question 4
En déduire le signe de sur .
Correction
Sur , la fonction est continue et strictement croissante et .
Donc pour tout et pour tout .
On résume cela dans un tableau de signe :

Donc pour tout et pour tout .
On résume cela dans un tableau de signe :

Question 5
Soit la fonction définie sur par .
Démontrer que, pour tout réel , .
Correction
Soit :
est dérivable sur
Ici on reconnait la forme avec et .
Attention : pour , lorsque nous allons faire sa dérivée il faudra utiliser la forme .
Ainsi et .
Il vient alors que :
équivaut successivement à
est dérivable sur
Ici on reconnait la forme avec et .
Attention : pour , lorsque nous allons faire sa dérivée il faudra utiliser la forme .
Ainsi et .
Il vient alors que :
Question 6
Etudier le sens de variations de la fonction (les limites de la fonction ne sont pas demandées).
Correction
Pour tout réel , on a et
Comme , il en résulte que le signe de est le même que celui de .
D'après la question , nous avons vu que : On en déduit facilement le tableau de variation de la fonction
On en déduit facilement le tableau de variation de la fonction
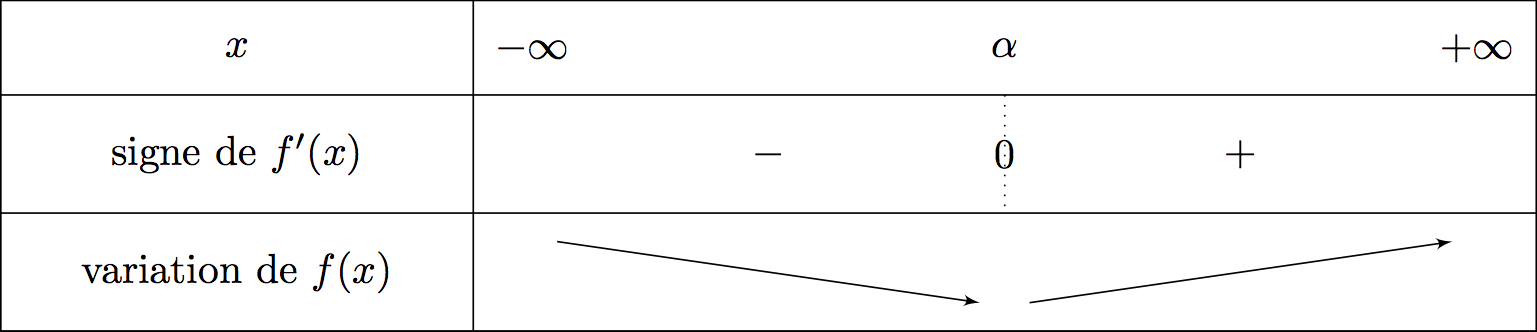
Comme , il en résulte que le signe de est le même que celui de .
D'après la question , nous avons vu que :

