Etude de fonctions - Exercice 5

20 min
35
Question 1
On considère la fonction ff définie sur R\mathbb{R} par : f(x)=12+3e−xf\left(x\right)=\frac{1}{2+3e^{-x} }

Calculer la limite de ff en −∞-\infty. Que peut-on en déduire graphiquement?

Correction
Ici, il s'agit d'une limite par composition.
On commence par calculer lim⁡x→−∞−x=+∞\lim\limits_{x\to -\infty } -x=+\infty .
On pose X=−xX=-x.
Ainsi : lim⁡X→+∞eX=+∞\lim\limits_{X\to +\infty } e^{X} =+\infty.
Par composition :
lim⁡x→−∞e−x=+∞\lim\limits_{x\to -\infty } e^{-x} =+\infty

lim⁡x→−∞1=1lim⁡x→−∞2+3e−x=+∞}par quotient\left. \begin{array}{ccc} {\lim\limits_{x\to -\infty } 1} & {=} & {1} \\ {\lim\limits_{x\to -\infty } 2+3e^{-x}} & {=} & {+\infty } \end{array}\right\}{\text{par quotient}}
lim⁡x→−∞12+3e−x=0\lim\limits_{x\to -\infty } \frac{1}{2+3e^{-x} }=0
Si lim⁡x→+∞f(x)=l\lim\limits_{x\to +\infty } f(x) =l où ll est une valeur finie alors la fonction ff admet une asymptote horizontale d'équation y=ly=l
Si lim⁡x→−∞f(x)=l\lim\limits_{x\to -\infty } f(x) =l où ll est une valeur finie alors la fonction ff admet une asymptote horizontale d'équation y=ly=l
La courbe CfC_{f} admet au voisinage de −∞-\infty une asymptote horizontale d'équation y=0y=0.
Question 2

Calculer la limite de ff en +∞+\infty. Que peut-on en déduire graphiquement?

Correction
Ici, il s'agit d'une limite par composition.
On commence par calculer lim⁡x→+∞−x=−∞\lim\limits_{x\to +\infty } -x=-\infty .
On pose X=−xX=-x.
Ainsi : lim⁡X→−∞eX=0\lim\limits_{X\to -\infty } e^{X} =0.
Par composition :
lim⁡x→+∞e−x=0\lim\limits_{x\to +\infty } e^{-x} =0

lim⁡x→+∞1=1lim⁡x→+∞2+3e−x=2}par quotient\left. \begin{array}{ccc} {\lim\limits_{x\to +\infty } 1} & {=} & {1} \\ {\lim\limits_{x\to +\infty } 2+3e^{-x}} & {=} & {2 } \end{array}\right\}{\text{par quotient}}
lim⁡x→+∞12+3e−x=12\lim\limits_{x\to +\infty } \frac{1}{2+3e^{-x} }=\frac{1}{2}
Si lim⁡x→+∞f(x)=l\lim\limits_{x\to +\infty } f(x) =l où ll est une valeur finie alors la fonction ff admet une asymptote horizontale d'équation y=ly=l
Si lim⁡x→−∞f(x)=l\lim\limits_{x\to -\infty } f(x) =l où ll est une valeur finie alors la fonction ff admet une asymptote horizontale d'équation y=ly=l
La courbe CfC_{f} admet au voisinage de +∞+\infty une asymptote horizontale d'équation y=12y=\frac{1}{2}.
Question 3

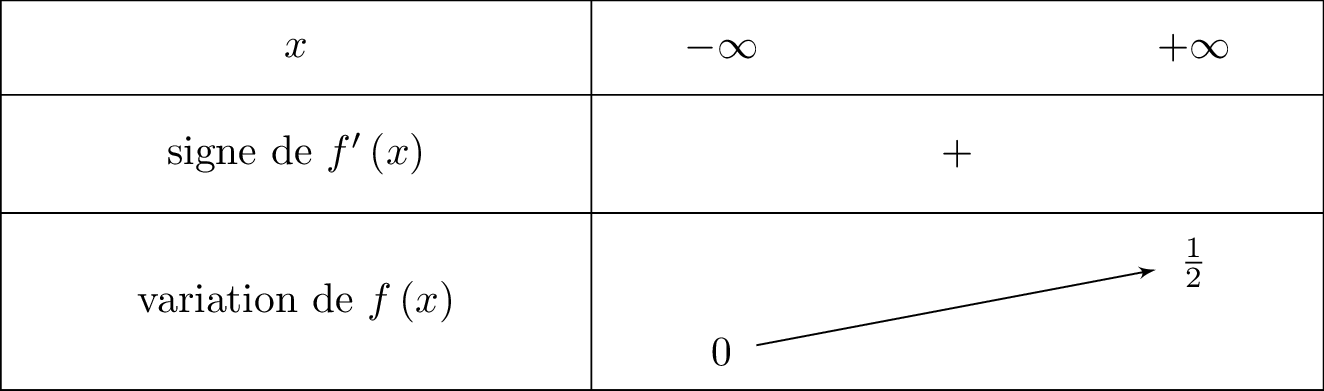
Etudier les variations de ff.

Correction
ff est dérivable sur R\mathbb{R}.
Ici on reconnaît la forme (1v)′=−v′v2\left(\frac{1}{v} \right)^{'} =\frac{-v'}{v^{2} } avec v(x)=2+3e−xv\left(x\right)=2+3e^{-x} .
Ainsi v′(x)=−3e−xv'\left(x\right)=-3e^{-x} .
f′(x)=−−3e−x(2+3e−x)2f'\left(x\right)=-\frac{-3e^{-x} }{\left(2+3e^{-x} \right)^{2} }
Il vient alors que :
f′(x)=3e−x(2+3e−x)2f'\left(x\right)=\frac{3e^{-x} }{\left(2+3e^{-x} \right)^{2} }

Pour tout réel xx, on vérifie aisément que : (2+3e−x)2>0\left(2+3e^{-x} \right)^{2}>0. De plus , e−x>0e^{-x}>0 et donc que 3e−x>03e^{-x}>0.
Il en résulte donc que pour tout réel xx, on a : f′(x)>0f'\left(x\right)>0. La fonction ff est donc croissante sur R\mathbb{R}.

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.