La fonction exponentielle
Etude de fonctions - Exercice 3
15 min
20
Etudiez les variations des fonctions suivantes sur .
Il faut avoir vu la fonction logarithme népérien pour pouvoir faire cet exercice.
Question 1
Correction
est dérivable sur . On a :
Résolvons l'inéquation :
équivaut successivement à :
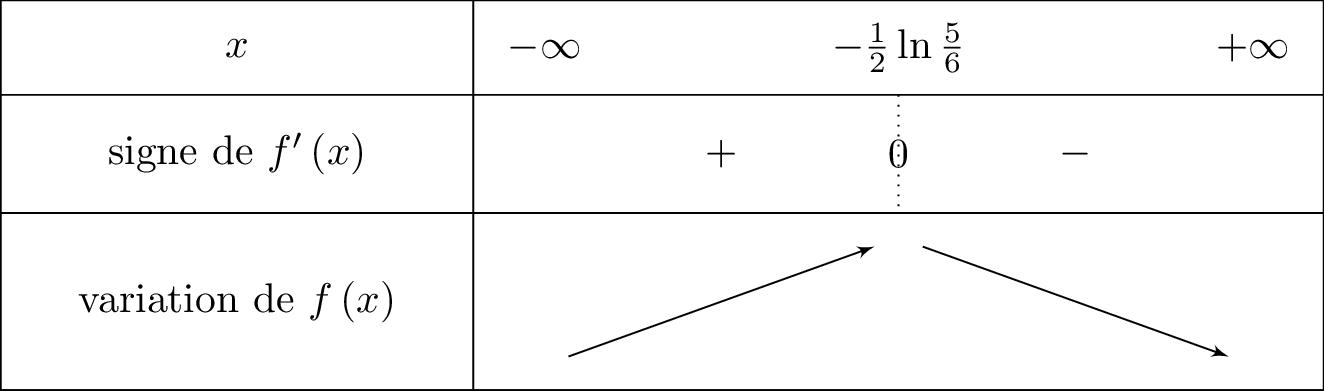
Cela signifie que lorsque . Nous traduisons cela dans un tableau de variation, ainsi :
Résolvons l'inéquation :
équivaut successivement à :
Cela signifie que lorsque . Nous traduisons cela dans un tableau de variation, ainsi :

Question 2
Correction
- avec
est dérivable sur .
On a :
Résolvons l'inéquation :
équivaut successivement à :
Cela signifie que lorsque .
Nous mettrons donc le signe lorsque .
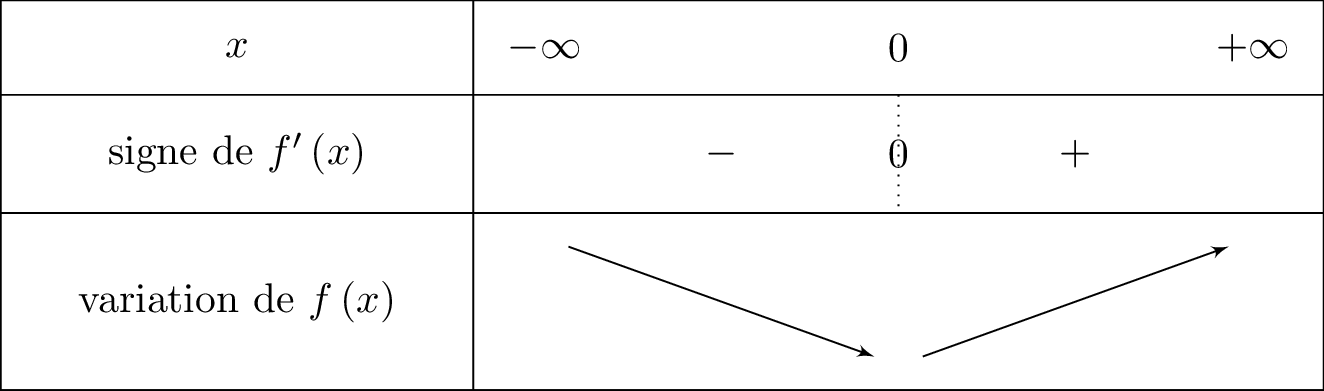
Nous traduisons cela dans un tableau de variation, ainsi :
Question 3
Correction
- avec
est dérivable sur .
On a :
Résolvons l'inéquation :
équivaut successivement à :
Cela signifie que lorsque .
Nous mettrons donc le signe lorsque .
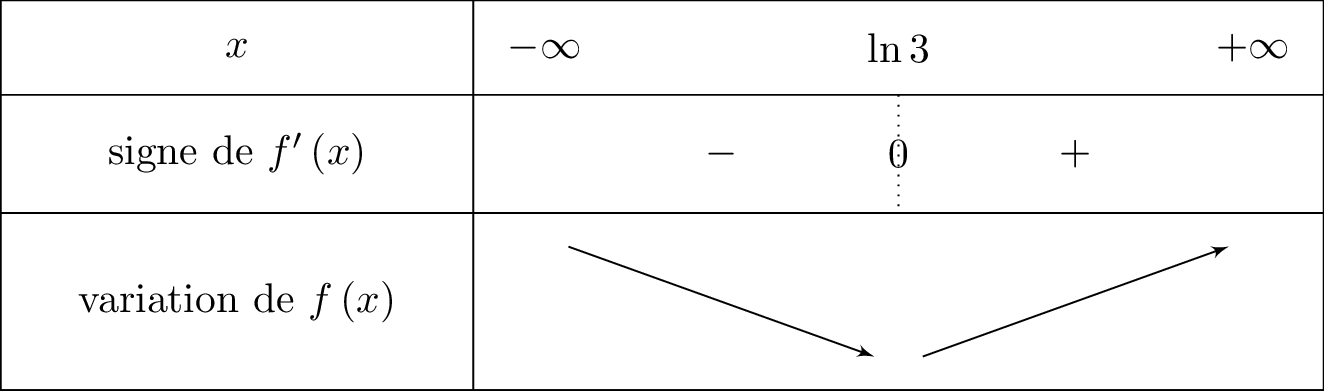
Nous traduisons cela dans un tableau de variation, ainsi :
Question 4
Correction
- avec
est dérivable sur
On a :
Résolvons l'inéquation :
équivaut successivement à :
Cela signifie que lorsque .
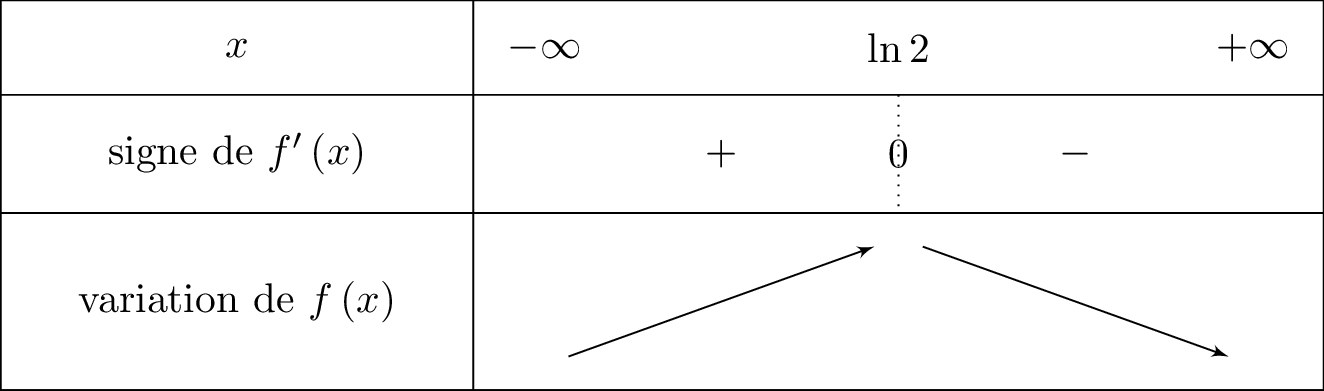
Nous traduisons cela dans un tableau de variation, ainsi :