La fonction exponentielle

A la mode au bac : des exponentielles et des sciences physiques - Exercice 3

35 min
55
On s’intéresse à la chute d’une goutte d’eau qui se détache d’un nuage sans vitesse initiale. Un modèle très simplifié permet d’établir que la vitesse instantanée verticale, exprimée en m.s−1m.s^{-1}, de chute de la goutte en fonction de la durée de chute tt est donnée par la fonction vv définie ainsi :
Pour tout réel positif ou nul tt, v(t)=9,81mk(1−e−kmt)v\left(t\right)=9,81\frac{m}{k} \left(1-e^{-\frac{k}{m} t} \right).
  • La constante mm est la masse de la goutte en milligramme et la constante kk est un coefficient strictement positif lié au frottement de l’air.
    • Question 1
    On rappelle que la vitesse instantanée est la dérivée de la position.
    Les parties AA et BB sont indépendantes.
    Partie A. Cas général

    Déterminer les variations de la vitesse de la goutte d’eau.

    Correction
    vv est dérivable sur [0;+∞[\left[0;+\infty \right[. Pour tout réel tt positif, on a :
    v′(t)=9,81mk×(−(−km)×e−kmt)v'\left(t\right)=9,81\frac{m}{k} \times \left(-\left(-\frac{k}{m} \right)\times e^{-\frac{k}{m} t} \right)
    v′(t)=9,81mk×kme−kmtv'\left(t\right)=9,81\frac{m}{k} \times \frac{k}{m} e^{-\frac{k}{m} t}
    v′(t)=9,81e−kmtv'\left(t\right)=9,81e^{-\frac{k}{m} t}
    Or, 9,81>09,81>0 et e−kmt>0e^{-\frac{k}{m} t}>0. Il en résulte que v′(t)>0v'\left(t\right)>0. Le tableau de variation est donnée ci-dessous :
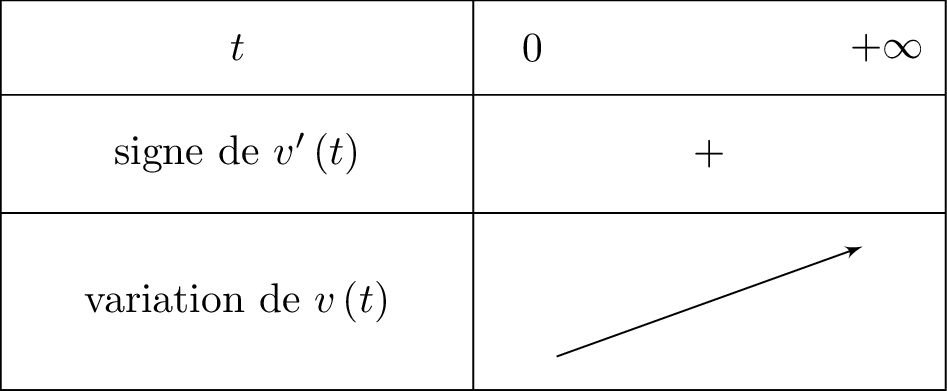    On en déduit que la vitesse de la goutte est strictement croissante sur [0;+∞[\left[0;+\infty \right[.
    Question 2

    La goutte ralentit-elle au cours de sa chute?

    Correction
    Sa vitesse étant strictement croissante, la goutte ne ralentit pas.
    Question 3

    Montrer que lim⁡t→+∞v(t)=9,81mk\lim\limits_{t\to +\infty } v\left(t\right)=9,81\frac{m}{k}. Cette limite s’appelle vitesse limite de la goutte.

    Correction
    Ici, il s'agit d'une limite par composition.
    v(t)=9,81mk(1−e−kmt)v\left(t\right)=9,81\frac{m}{k} \left(1-e^{-\frac{k}{m} t} \right)
    On commence par calculer lim⁡t→+∞−kmt=−∞\lim\limits_{t\to +\infty } -\frac{k}{m} t=-\infty .
    On pose T=−kmtT=-\frac{k}{m} t.
    Ainsi : lim⁡T→−∞eT=0\lim\limits_{T\to -\infty } e^{T} =0.
    Par composition :
    lim⁡t→+∞e−kmt=0\lim\limits_{t\to +\infty } e^{-\frac{k}{m} t} =0

    Finalement :
    lim⁡t→+∞9,81mk(1−e−kmt)=9,81mk\lim\limits_{t\to +\infty } 9,81\frac{m}{k} \left(1-e^{-\frac{k}{m} t} \right) =9,81\frac{m}{k}
    Question 4

    Un scientifique affirme qu’au bout d’une durée de chute égale à 5mk\frac{5m}{k} , la vitesse de la goutte dépasse 99%99\% de sa vitesse limite. Cette affirmation est-elle correcte?

    Correction
    Commençons par calculer v(5mk)v\left(\frac{5m}{k}\right).
    v(5mk)=9,81mk(1−e−km×5mk)v\left(\frac{5m}{k}\right)=9,81\frac{m}{k} \left(1-e^{-\frac{k}{m}\times\frac{5m}{k}} \right) équivaut successivement à :
    v(5mk)=9,81mk(1−e−5)v\left(\frac{5m}{k}\right)=9,81\frac{m}{k} \left(1-e^{-5} \right)
    Faisons maintenant le rapport de v(5mk)v\left(\frac{5m}{k}\right) sur le rapport de la vitesse limite 9,81mk9,81\frac{m}{k}.
    Il en résulte donc que :
    v(5mk)9,81mk=9,81mk(1−e−5)9,81mk=1−e−5≈0,993≈99,3%\frac{v\left(\frac{5m}{k} \right)}{9,81\frac{m}{k} } =\frac{9,81\frac{m}{k} \left(1-e^{-5} \right)}{9,81\frac{m}{k} } =1-e^{-5} \approx 0,993\approx 99,3\%.
    Cette vitesse dépasse 99%99\% de la vitesse limite. On en déduit que le scientifique a raison.
    Question 5
    Partie B.
    Dans cette partie, on prend m=6m = 6 et k=3,9k = 3,9. À un instant donné, la vitesse instantanée de cette goutte est 1515 m.s−1m.s^{-1} .

    Depuis combien de temps la goutte s’est-elle détachée de son nuage? Arrondir la réponse au dixième de seconde.

    Correction
    on prend m=6m = 6 et k=3,9k = 3,9, ce qui nous donne : mk=63,9=2013\frac{m}{k} =\frac{6}{3,9} =\frac{20}{13}
    Ainsi : v(t)=9,81×2013(1−e−1320t)v\left(t\right)=9,81\times \frac{20}{13} \left(1-e^{-\frac{13}{20} t} \right)
    Nous voulons résoudre : v(t)=15v\left(t\right)=15
    9,81×2013(1−e−1320t)=159,81\times \frac{20}{13} \left(1-e^{-\frac{13}{20} t} \right)=15 équivaut successivement à :
    9,81×(1−e−1320t)=15×13209,81\times \left(1-e^{-\frac{13}{20} t} \right)=15\times\frac{13}{20}
    9,81×(1−e−1320t)=3949,81\times \left(1-e^{-\frac{13}{20} t} \right)=\frac{39}{4}
    9,81×(1−e−1320t)=9,759,81\times \left(1-e^{-\frac{13}{20} t} \right)=9,75
    1−e−1320t=9,759,81 1-e^{-\frac{13}{20} t}=\frac{9,75}{9,81}
    −e−1320t=9,759,81−1 -e^{-\frac{13}{20} t}=\frac{9,75}{9,81}-1
    e−1320t=−9,759,81+1 e^{-\frac{13}{20} t}=-\frac{9,75}{9,81}+1
    ln⁡(e−1320t)=ln⁡(1−9,759,81)\ln \left(e^{-\frac{13}{20} t} \right)=\ln \left(1-\frac{9,75}{9,81} \right)
    −1320t=ln⁡(1−9,759,81)-\frac{13}{20} t=\ln \left(1-\frac{9,75}{9,81} \right)
    t=ln⁡(1−9,759,81)(−1320)t=\frac{\ln \left(1-\frac{9,75}{9,81} \right)}{\left(\frac{-13}{20} \right)}
    t≈7,84t\approx 7,84

    La goutte s’est donc détachée depuis environ 7,87,8 secondes quand sa vitesse atteint 1515 m.s−1m.s^{-1}
    Question 6

    En déduire la vitesse moyenne de cette goutte entre le moment où elle s’est détachée du nuage et l’instant où on a mesuré sa vitesse. Arrondir la réponse au dixième de m.s−1m.s^{-1} .

    Correction
    Soit ff une fonction continue sur un intervalle [a;b]\left[a;b\right].
    La valeur moyenne de la fonction ff sur [a;b]\left[a;b\right] est le réel mm défini par : m=1b−a∫abf(x)dxm=\frac{1}{b-a} \int _{a}^{b}f\left(x\right) dx
    On cherche la valeur moyenne de v(t)v\left(t\right) sur l'intervalle [0;7,8]\left[0; 7,8\right].
    Cette valeur moyenne est donnée par :
    m=17,8−0∫abv(t)dtm=\frac{1}{7,8-0} \int _{a}^{b}v\left(t\right) dt
    m=17,8−0×9,81×2013∫07,81−e−1320tdtm=\frac{1}{7,8-0} \times 9,81\times \frac{20}{13} \int _{0}^{7,8}1-e^{-\frac{13}{20} t} dt
  • Une primitive de eax+be^{ax+b} est 1aeax+b\frac{1}{a} e^{ax+b}
    • m=327169[t+2013e−1320t]07,8m=\frac{327}{169} \left[t+\frac{20}{13} e^{-\frac{13}{20} t} \right]_{0}^{7,8}
    m=327169(7,8+2013e−1320×7,8−0−2013e−1320×0)m=\frac{327}{169} \left(7,8+\frac{20}{13} e^{-\frac{13}{20} \times 7,8} -0-\frac{20}{13} e^{-\frac{13}{20} \times 0} \right)
    m=327169(7,8+2013e−5,07−2013)m=\frac{327}{169} \left(7,8+\frac{20}{13} e^{-5,07} -\frac{20}{13} \right)
    m≈12,1m\approx 12,1

    La vitesse moyenne de la goutte est donc d’environ 12,112,1 m.s−1m.s^{-1} sur l'intervalle [0;7,8]\left[0; 7,8\right].