A la mode au bac : des exponentielles et des sciences physiques - Exercice 2

La demi-vie du médicament est la durée ( en heure ) après laquelle la concentration plasmatique du médicament est égale à la moitié de la concentration initiale. Il nous faut donc calculer $$f\left(t\right)=10$$.
$$f\left(t\right)=10$$ équivaut successivement à :
$$20e^{-0,1t} =10$$
$$e^{-0,1t} =\frac{10}{20}$$
$$e^{-0,1t} =\frac{1}{2}$$
$$\ln \left(e^{-0,1t} \right)=\ln \left(\frac{1}{2} \right)$$
$$-0,1t=\ln \left(\frac{1}{2} \right)$$
$$-0,1t=-\ln \left(2\right)$$
$$t=\frac{-\ln \left(2\right)}{-0,1}$$
$$t=\frac{\ln \left(2\right)}{0,1}$$

La demi-vie est d’environ $$6,9$$ heures soit $$6$$ heures et $$54$$ minutes.

On estime que le médicament est éliminé dès que la concentration plasmatique est inférieure à $$0,2$$ $$\mu g.L^{-1}$$.
Résolvons alors : $$f\left(t\right)\le 0,2$$
$$f\left(t\right)\le 0,2$$ équivaut successivement à :
$$20e^{-0,1t} \le 0,2$$
$$e^{-0,1t} \le \frac{0,2}{20}$$
$$e^{-0,1t} \le 0,01$$
$$\ln \left(e^{-0,1t} \right)\le \ln \left(0,01\right)$$
$$\ln \left(e^{-0,1t} \right)\le \ln \left(0,01\right)$$
$$-0,1t\le \ln \left(0,01\right)$$
$$t\ge \frac{\ln \left(0,01\right)}{-0,1}$$

Le médicament est éliminé au bout de $$46,1$$ heures (soit $$46$$ heures et $$6$$ min).

$$\red{\text{ D'une part :}}$$
$$\int _{0}^{x}f\left(t\right)dt =\int _{0}^{x}20e^{-0,1t} dt$$
$$\int _{0}^{x}f\left(t\right)dt =\left[20\times \frac{1}{-0,1} e^{-0,1t} \right]_{0}^{x}$$
$$\int _{0}^{x}f\left(t\right)dt =\left[-200e^{-0,1t} \right]_{0}^{x}$$
$$\int _{0}^{x}f\left(t\right)dt =-200e^{-0,1x} -\left(-200e^{-0,1\times 0} \right)$$
$$\int _{0}^{x}f\left(t\right)dt =-200e^{-0,1x} -\left(-200e^{0} \right)$$
$$\int _{0}^{x}f\left(t\right)dt =-200e^{-0,1x} -\left(-200\right)$$

$$\red{\text{ D'autre part :}}$$
$$\lim\limits_{x\to +\infty }\int _{0}^{x}f\left(t\right)dt=\lim\limits_{x\to +\infty }-200e^{-0,1x} +200$$
On commence par calculer $$\lim\limits_{x\to +\infty } -0,1x=-\infty$$.
On pose $$X=-0,1x$$.
Ainsi : $$\lim\limits_{X\to -\infty } e^{X} =0$$.
Par composition :
D'où :

DOnc l’ASC est égal à $$200$$ $$\mu g.L^{-1}$$.

Soit : $$g\left(t\right)=20\left(e^{-0,1t} -e^{-t} \right)$$
$$g$$ est dérivable sur $$\left[0;+\infty\right[$$.
$$g'\left(t\right)=20\left(-0,1e^{-0,1t} +e^{-t} \right)$$. Nous allons factoriser par $$e^{-t}$$ .
$$g'\left(t\right)=20e^{-t} \left(\frac{-0,1e^{-0,1t} +e^{-t} }{e^{-t} } \right)$$
$$g'\left(t\right)=20e^{-t} \left(\frac{-0,1e^{-0,1t} }{e^{-t} } +\frac{e^{-t} }{e^{-t} } \right)$$
$$g'\left(t\right)=20e^{-t} \left(\frac{-0,1e^{-0,1t} }{e^{-t} } +1\right)$$
$$g'\left(t\right)=20e^{-t} \left(-0,1e^{-0,1t-\left(-t\right)} +1\right)$$
$$g'\left(t\right)=20e^{-t} \left(-0,1e^{-0,1t+t} +1\right)$$

Pour tout réel $$t\in\left[0;+\infty\right[$$, on vérifie aisément que $$20e^{-t}>0$$. Le signe de $$g'$$ est alors du signe de $$-0,1e^{0,9t} +1$$.
$$-0,1e^{0,9t} +1\ge 0$$
$$-0,1e^{0,9t} \ge -1$$
$$e^{0,9t} \le \frac{-1}{-0,1}$$
$$e^{0,9t} \le 10$$
$$\ln \left(e^{0,9t} \right)\le \ln \left(10\right)$$
$$0,9t\le \ln \left(10\right)$$

Il en résulte donc que :

• si $$t\in\left[0;\frac{\ln \left(10\right)}{0,9}\right]$$ alors $$g'\left(t\right)\ge0$$ et donc $$g$$ est croissante sur cet intervalle.
• si $$t\in\left[\frac{\ln \left(10\right)}{0,9};+\infty\right[$$ alors $$g'\left(t\right)\le0$$ et donc $$g$$ est décroissante sur cet intervalle.

De plus : $$g\left(\frac{\ln \left(10\right)}{0,9}\right)\approx13,94$$
Nous traduisons toutes ces informations dans le tableau de variation ci-dessous :
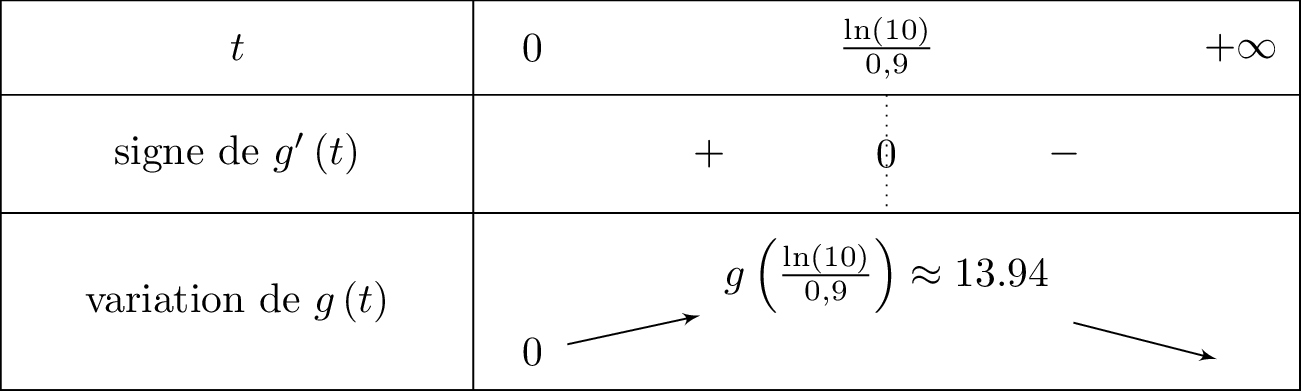La durée après laquelle la concentration est maximale est $$\frac{\ln \left(10\right)}{0,9}$$ h , soit environ $$2$$ h $$34$$ min.

Nous allons procéder par récurrence.
Pour tout entier naturel $$n$$, posons la propriété $$P_{n} :u_{n}=40-40\times 0,5^{n}$$
Etape d'initialisation
On sait que $$u_{1} =20$$ et que $$u_{1}=40-40\times 0,5^{1}=20$$ .
La propriété $$P_{0}$$ est vraie.
Etape d'hérédité
On suppose qu'il existe un entier $$k$$ tel que la propriété $$P_{k}$$ soit vraie c'est-à-dire $$u_{k}=40-40\times 0,5^{k}$$ et vérifions si la propriété est également vraie au rang $$k+1$$ c'est-à-dire $$u_{k+1}=40-40\times 0,5^{k+1}$$
Par hypothèse de récurrence :
$$u_{k}=40-40\times 0,5^{k}$$ , on multiplie par $$0,5$$ de part et d'autre de l'égalité
$$0,5u_{k} =0,5\times \left(40-40\times 0,5^{k} \right)$$
$$0,5u_{k} =0,5\times 40-40\times 0,5^{k} \times 0,5$$
$$0,5u_{k} =20-40\times 0,5^{k} \times 0,5$$ . On va maintenant additionner par $$20$$ de part et d'autre de l'égalité (notre objectif est de faire apparaître dans le membre de gauche $$u_{k+1}$$)
$$0,5u_{k}+20 =20-40\times 0,5^{k} \times 0,5+20$$
$$0,5u_{k}+20 =40-40\times {\color{blue}0,5^{k} \times 0,5}$$

Ainsi la propriété $$P_{k+1}$$ est vraie.
Conclusion
Puisque la propriété $$P_{0}$$ est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel $$n$$, on a $$P_{n}$$ vraie, c'est à dire que pour tout entier naturel $$n$$, on a bien :

Comme $$-1<0,5<1$$ alors :
$$\lim\limits_{n\to +\infty } \left(0,5\right)^{n} =0$$
$$\lim\limits_{n\to +\infty } \left(-40\right)\times \left(0,5\right)^{n} =0$$
$$\lim\limits_{n\to +\infty } \left(-40\right)\times \left(0,5\right)^{n} +40=40$$
Ainsi :

On cherche l’entier $$n$$ minimum tel que $$u_{n}\ge38$$.
$$40-40\times 0,5^{n} \ge 38$$
$$-40\times 0,5^{n} \ge 38-40$$
$$-40\times 0,5^{n} \ge -2$$
$$0,5^{n} \le \frac{-2}{-40}$$
$$0,5^{n} \le 0,05$$
$$\ln \left(0,5^{n} \right)\le \ln \left(0,05\right)$$
$$n\ln \left(0,5\right)\le \ln \left(0,05\right)$$
$$n\ge \frac{\ln \left(0,05\right)}{\ln \left(0,5\right)}$$ . Comme $$\ln \left(0,5\right)<0$$, il faut changer le sens de l'inéquation.

Il faut donc au minimum $$5$$ injections.