Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Lien entre une chaîne de Markov et distributions - Exercice 1
10 min
20
Question 1
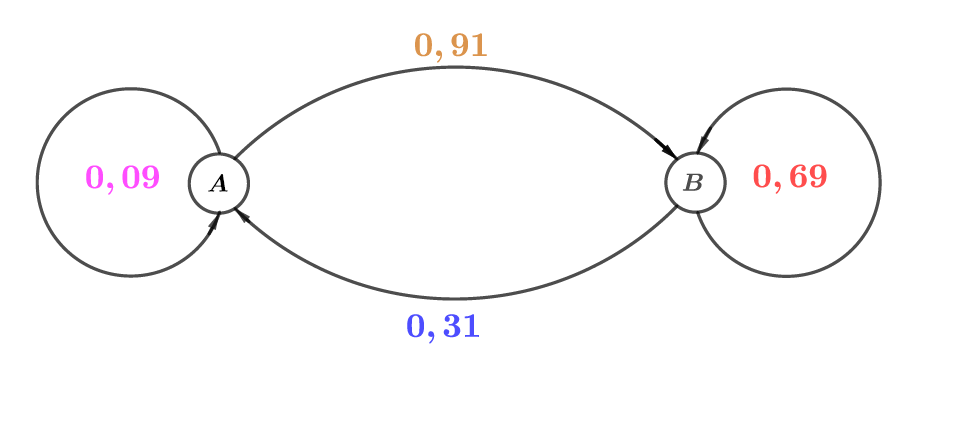
Donner la matrice de transition associé de cette chaîne de Markov.
Correction
Nous avons alors :
Question 2
Calculer à l'aide de la calculatrice.
Correction
D'après la calculatrice, nous obtenons :
Question 3
Déterminer la probabilité de passer de l'état à l'état en deux étapes .
Correction
Pour déterminer la probabilité de passer de l'état à l'état en deux étapes, il faut tout d'abord calculer .
A l'aide de la question , nous connaissons désormais .
Il faut maintenant lire dans la matrice la valeur étant l'intersection entre la première ligne ( en référence à ) et la deuxième colonne ( en référence à ) . En effet, nous voulons passer de l'état à l'état .
Il vient alors que la probabilité est alors de
A l'aide de la question , nous connaissons désormais .
Il faut maintenant lire dans la matrice la valeur étant l'intersection entre la première ligne ( en référence à ) et la deuxième colonne ( en référence à ) . En effet, nous voulons passer de l'état à l'état .
Il vient alors que la probabilité est alors de
Question 4
D'après la distribution initiale , nous savons que nous avons de chance de démarrer à l'état .
Calculer la probabilité qu'à la deuxième étape nous soyons encore à l'état .
Correction
La distribution donnera les probabilités relatives à l'état et à l'état lors de la deuxième étape.
La probabilité qu'à la deuxième étape nous soyons encore à l'état est alors de : . Approximativement, il y a de chance d'étre à l'état à la deuxième étape.
La probabilité qu'à la deuxième étape nous soyons encore à l'état est alors de : . Approximativement, il y a de chance d'étre à l'état à la deuxième étape.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.