Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Savoir utiliser la matrice d'adjacence d'un graphe - Exercice 1
6 min
10
On considère le graphe représenté ci-dessous :
Question 1
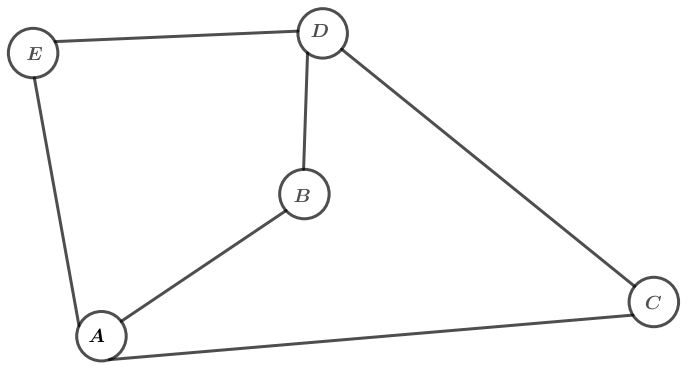
Donner la matrice d’adjacence du graphe (les sommets seront rangés dans l’ordre alphabétique)
Correction
Question 2
A l'aide de la calculatrice, donner .
Correction
D'après la calculatrice, on obtient :
Question 3
Combien y'a-t-il de chemins de longueur reliant à .
Correction
Soit un graphe et sa matrice d’adjacence.
Le nombre de chemins de longueur joignant le sommet au sommet est donné par le terme d’indice de la matrice
Pour déterminer le nombre de chemins de longueur reliant le sommet au sommet sommet , on doit calculer . D'après la question , nous connaissons .Le nombre de chemins de longueur joignant le sommet au sommet est donné par le terme d’indice de la matrice
Nous allons prendre la valeur de l'intersection entre la deuxième ligne ( en référence au sommet ) et de la troisième colonne ( en référence au sommet )
Nous mettons cette valeur dans la matrice
Il y a donc chemins de longueur reliant le sommet au sommet .
Question 4
A l'aide de la calculatrice, donner .
Correction
D'après la calculatrice, on obtient :
Question 5
Combien y'a-t-il de chemins de longueur reliant à .
Correction
Soit un graphe et sa matrice d’adjacence.
Le nombre de chemins de longueur joignant le sommet au sommet est donné par le terme d’indice de la matrice
Pour déterminer le nombre de chemins de longueur reliant le sommet au sommet sommet , on doit calculer . D'après la question , nous connaissons .Le nombre de chemins de longueur joignant le sommet au sommet est donné par le terme d’indice de la matrice
Nous allons prendre la valeur de l'intersection entre la première ligne ( en référence au sommet ) et de la cinquième colonne ( en référence au sommet )
Nous mettons cette valeur dans la matrice
Il y a donc chemins de longueur reliant le sommet au sommet .
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.