Nouveau

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Matrices et transformations géométriques dans le plan : La symétrie axiale par rapport à l'axe des abscisses - Exercice 3

3 min
5
Question 1

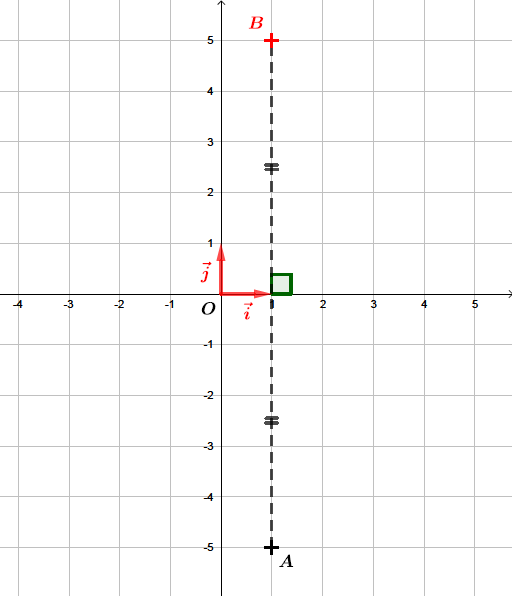
Dans un repère orthonormé direct (O;i→;j→)\left(O;\overrightarrow{i} ;\overrightarrow{j} \right), on donne le point A(1;−5)A\left(1;-5\right) .
Déterminer les coordonnées du point BB image du point AA par la symétrie axiale par rapport à l'axe des abscisses.

Correction
On se place dans un repère orthonormé direct (O;i→;j→)\left(O;\overrightarrow{i} ;\overrightarrow{j} \right) du plan.
  • Soient A(xA;yA)A\left(x_{A}; y_{A}\right) et B(xB;yB)B\left(x_{B}; y_{B}\right) deux points du plan .
  • BB est l'image de AA par symeˊtrie axiale par rapport aˋ l’axe des abscisses\red{\text{symétrie axiale par rapport à l'axe des abscisses}} si et seulement si (xByB)=(100−1)×(xAyA)\left(\begin{array}{c} {x_{B} } \\ {y_{B} } \end{array}\right)=\left(\begin{array}{cc} {1} & {0} \\ {0} & {-1} \end{array}\right)\times \left(\begin{array}{c} {x_{A} } \\ {y_{A} } \end{array}\right)
    • Il nous suffit d'appliquer la formule du rappel. Il vient alors que :
    (xByB)=(100−1)×(xAyA)\left(\begin{array}{c} {x_{B} } \\ {y_{B} } \end{array}\right)=\left(\begin{array}{cc} {1} & {0} \\ {0} & {-1} \end{array}\right)\times \left(\begin{array}{c} {x_{A} } \\ {y_{A} } \end{array}\right)
    (xByB)=(100−1)×(1−5)\left(\begin{array}{c} {x_{B} } \\ {y_{B} } \end{array}\right)=\left(\begin{array}{cc} {{\color{blue}{1}}} & {{\color{blue}{0}}} \\ {{\color{red}{0}}} & {{\color{red}{-1}}} \end{array}\right)\times \left(\begin{array}{c} {{\color{green}{1}} } \\ {{\color{green}{-5}} } \end{array}\right)
    (xByB)=(1×1+0×(−5)0×1+(−1)×(−5))\left(\begin{array}{c} {x_{B} } \\ {y_{B} } \end{array}\right)=\left(\begin{array}{c} {{\color{blue}{1}}\times {\color{green}{1}}+{\color{blue}{0}}\times {\color{green}{\left(-5\right)}}} \\ {{\color{red}{0}}\times \color{green}{1}+\left({\color{red}{-1}}\right)\times \left(-5\right)} \end{array}\right)
    (xByB)=(1+00+5)\left(\begin{array}{c} {x_{B} } \\ {y_{B} } \end{array}\right)=\left(\begin{array}{c} {1+0} \\ {0+5} \end{array}\right)
    Ainsi :
    (xByB)=(15)\left(\begin{array}{c} {x_{B} } \\ {y_{B} } \end{array}\right)=\left(\begin{array}{c} {1} \\ {5} \end{array}\right)

    Les coordonnées du point BB image du point AA par la symétrie axiale par rapport à l'axe des abscisses sont B(1;5)B\left(1;5\right)

    Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.