Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Matrices et transformations géométriques dans le plan : L'homothétie - Exercice 2
4 min
10
Question 1
Dans un repère orthonormé direct , on donne le point .
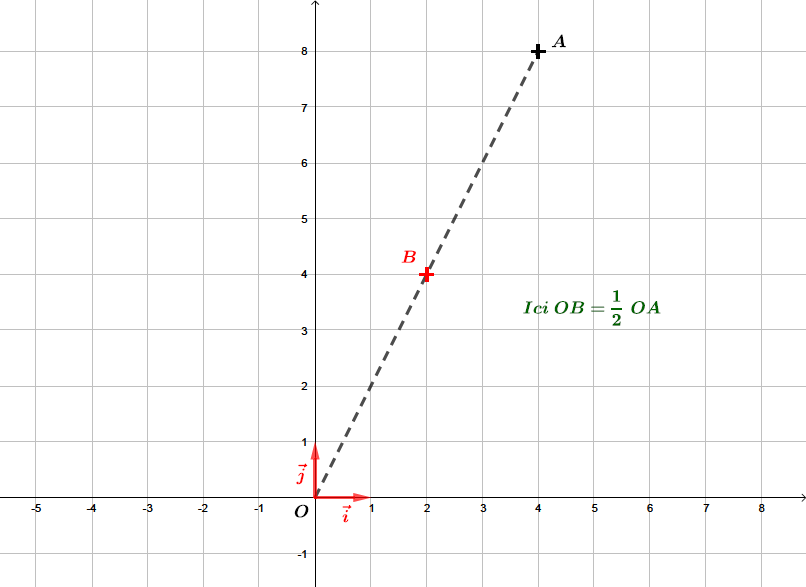
Déterminer les coordonnées du point image du point par l'homothétie de centre et de rapport .
Déterminer les coordonnées du point image du point par l'homothétie de centre et de rapport .
Correction
On se place dans un repère orthonormé direct du plan.Soient et deux points du plan et un réel. est l'image de par de centre et de rapport si et seulement si
La matrice associée à l'homothétie de centre et de rapport est : Nous appliquons la formule du rappel, il vient alors que :
Ainsi :
Les coordonnées du point image du point par l'homothétie de centre et de rapport sont
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.