Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : Lien entre la convexité et inégalités - Exercice 3
15 min
30
Soit la fonction définie sur par .
Question 1
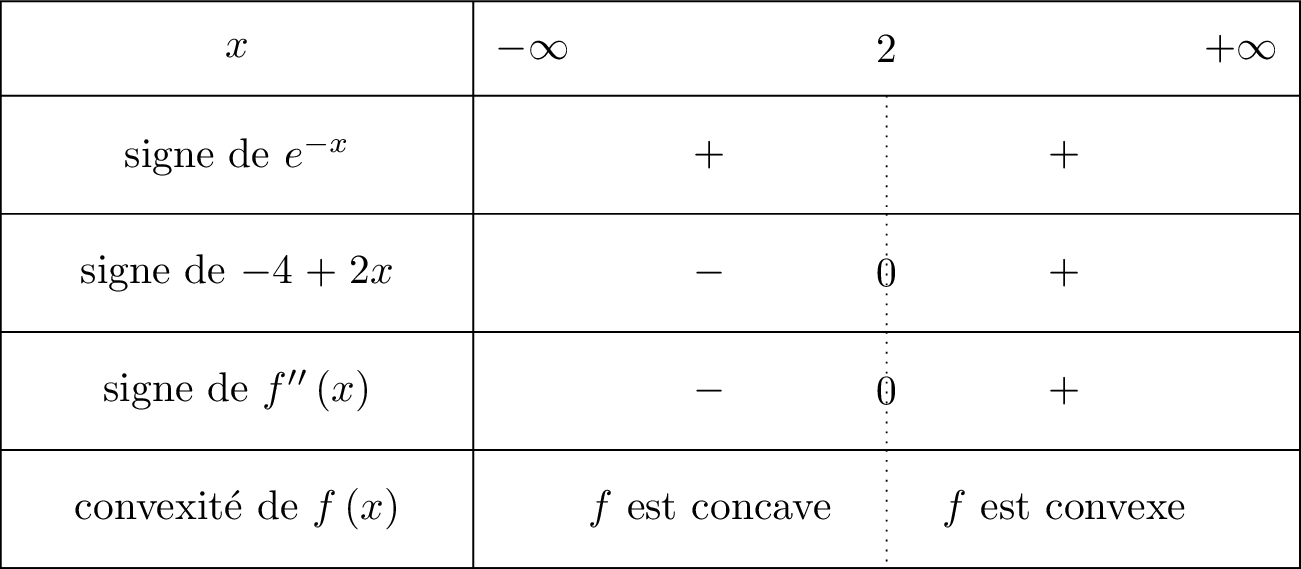
Etudiez la convexité de sur .
Correction
Ici on reconnaît la forme avec ; et
Ainsi : et , enfin
Il vient alors que :
Nous allons maintenant calculer .
Ici on reconnaît la forme avec ; et
Ainsi : et , enfin
Il vient alors que :
Finalement :
Pour tout réel , on a .
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera supérieur ou égale à .
- Lorsque sur un intervalle alors est convexe.
- Lorsque sur un intervalle alors est concave.
- si alors et donc est sur cet intervalle.
- si alors et donc est sur cet intervalle.
Question 2
Déterminer une équation de la tangente à au point d'abscisse .
Correction
L'équation de la tangente au point d'abscisse s'écrit .
Ici , ce qui donne, .calculer
calculer
on remplace les valeurs de et de dans la formule de l'équation de tangente.
On sait que :
Ainsi l'équation de la tangente à la courbe au point d'abscisse est alors .
Question 3
Pour tout réel en déduire que :
Correction
- Les deux définitions ci-dessous sont équivalentes :
Ainsi pour tout réel , on a :
Ce qui nous donne :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.