Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Tchat avec un prof
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Déterminer algébriquement les coordonnées des points d'inflexion d'une fonction - Exercice 2
5 min
15
On considère la fonction définie sur par .
On note la courbe représentative de la fonction .
On note la courbe représentative de la fonction .
Question 1
Déterminer algébriquement les coordonnées du (ou des) point(s) d'inflexion éventuel(s) de .
Correction
Pour étudier la convexité de la fonction , il faut étudier le signe de . Il va donc falloir calculer la dérivée seconde de .
est deux fois dérivable sur .
Il vient que :
et
Pour tout réel , on vérifie aisément que .
Il en résulte donc que :
Ainsi :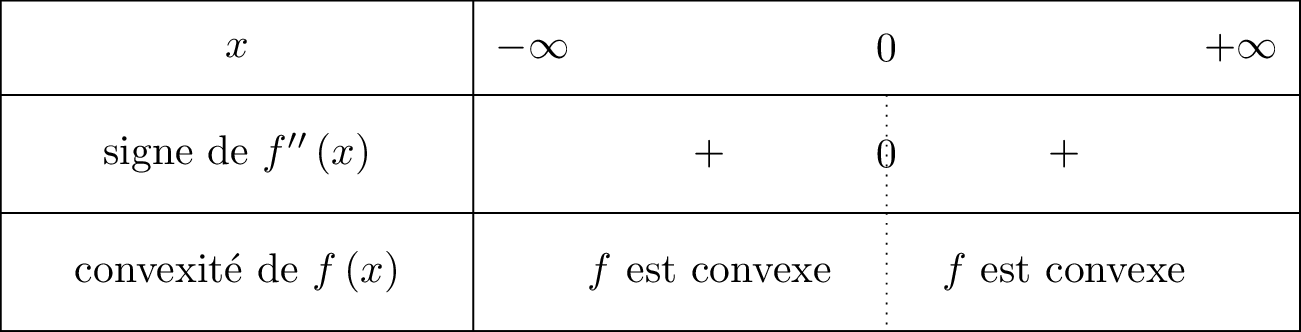 Dans cette situation, s'annule mais ne change pas de signe en .
Dans cette situation, s'annule mais ne change pas de signe en .
 Il en résulte donc qu'au point d'absicce la fonction n'admet pas de point d'inflexion.
Il en résulte donc qu'au point d'absicce la fonction n'admet pas de point d'inflexion.
La fonction n'admet donc pas de point d'inflexion sur .
est deux fois dérivable sur .
Il vient que :
et
- Lorsque sur un intervalle alors est convexe.
- Lorsque sur un intervalle alors est concave.
Il en résulte donc que :
- si alors et donc est sur cet intervalle.
Ainsi :
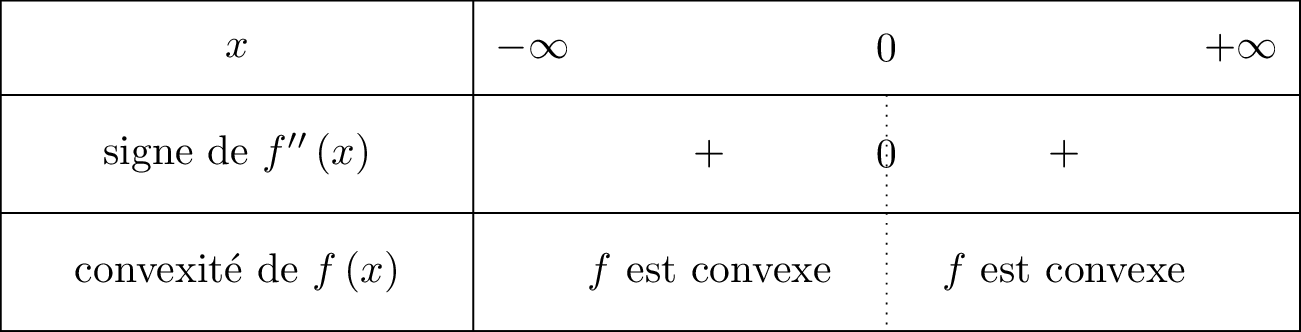
- possède un point d'inflexion lorsque sa dérivée seconde s'annule et change de signe en ce point.

La fonction n'admet donc pas de point d'inflexion sur .
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.