Qui aura 20 en maths ?

💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Probabilités conditionnelles - Exercice 6

18 min
30
Lors d'une enquête réalisée auprès de familles d'une région, on apprend que 40%40\% des familles ont 11 enfant, 40%40\% ont 22 enfants et enfin 20%20\% ont 33 enfants ou plus.
Toutes les familles interrogées vont en vacances chaque été.
6060% des familles avec 11 enfant vont à l’étranger, 8080% des familles avec 22 enfants restent en France et enfin 1515% des familles avec 33 enfants vont à l’étranger.
On interroge une famille de la région et on note :
  • FF l'événement : « la famille passe leurs vacances en France »
  • EE l'événement : « la famille passe leurs vacances à l'étranger »
  • AA l'événement : « la famille a un enfant »
  • BB l'événement : « la famille a deux enfants »
  • CC l'événement : « la famille a trois enfants »
Les probabilités seront données sous forme décimale, arrondies au millième.
Question 1

Dresser l'arbre pondéré traduisant cette situation.

Correction
On remplit l'arbre pondéré grâce aux informations données par l'énoncé.
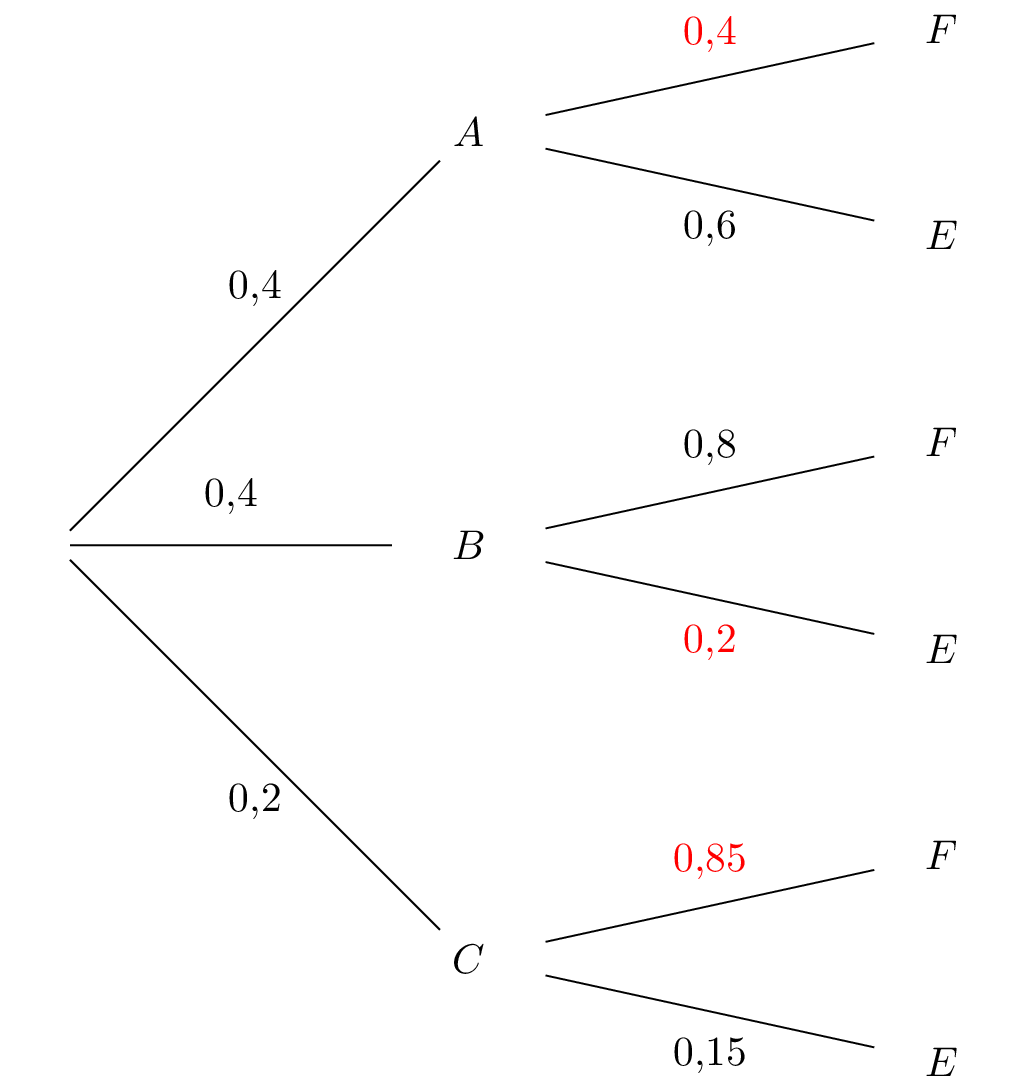
En noir les valeurs de l'énoncé et en rouge les valeurs que l'on déduit.
Question 2

Calculer la probabilité de l'événement : « la famille a deux enfants et passe ses vacances en France ».

Correction
On calcule :
P(B∩F)=P(B)×PB(F)P\left(B\cap F\right)=P\left(B\right)\times P_{B} \left(F\right)
P(B∩F)=0,4×0,8P\left(B\cap F\right)=0,4\times 0,8
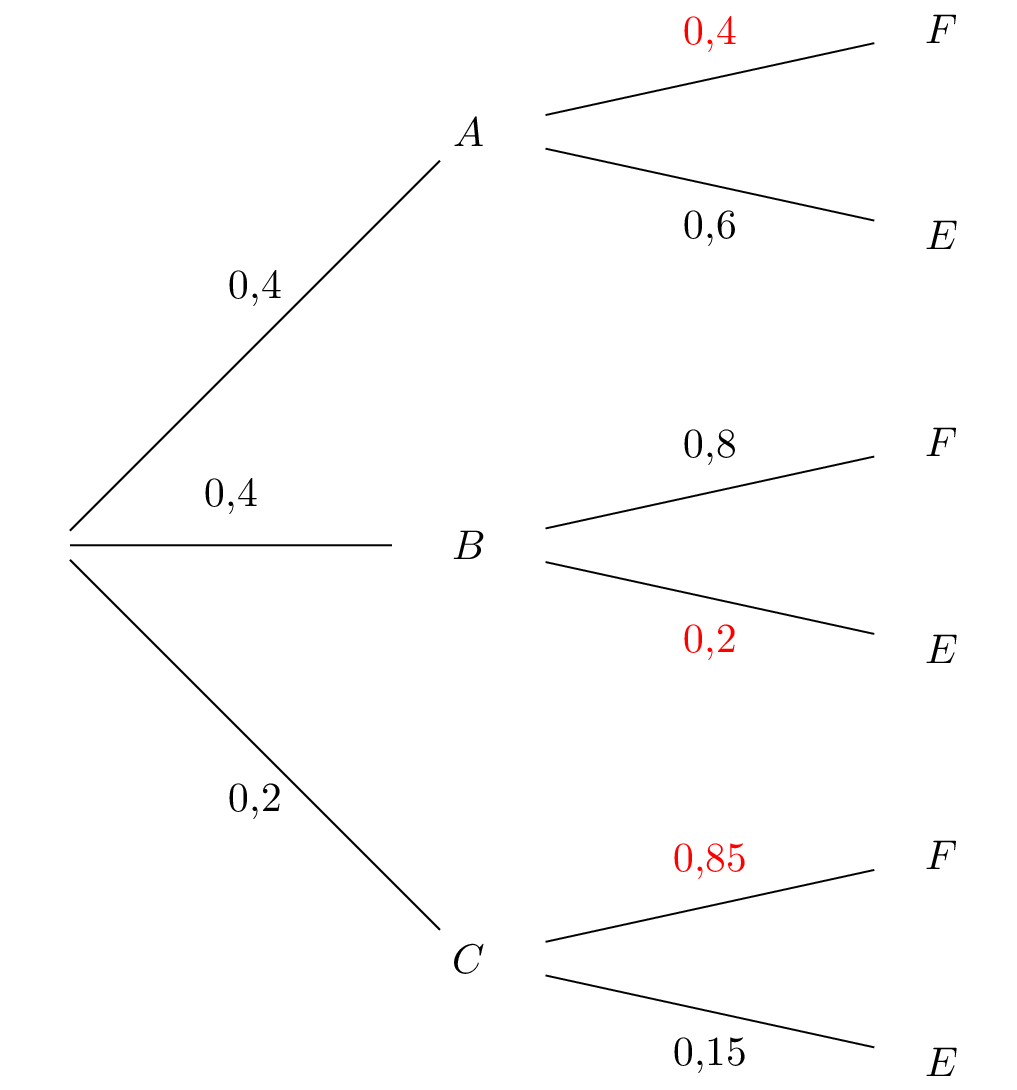
Soit :
P(B∩F)=0,32P\left(B\cap F\right)=0,32
Question 3

Montrer que la probabilité de l'événement FF est égale à 0,650,65.

Correction
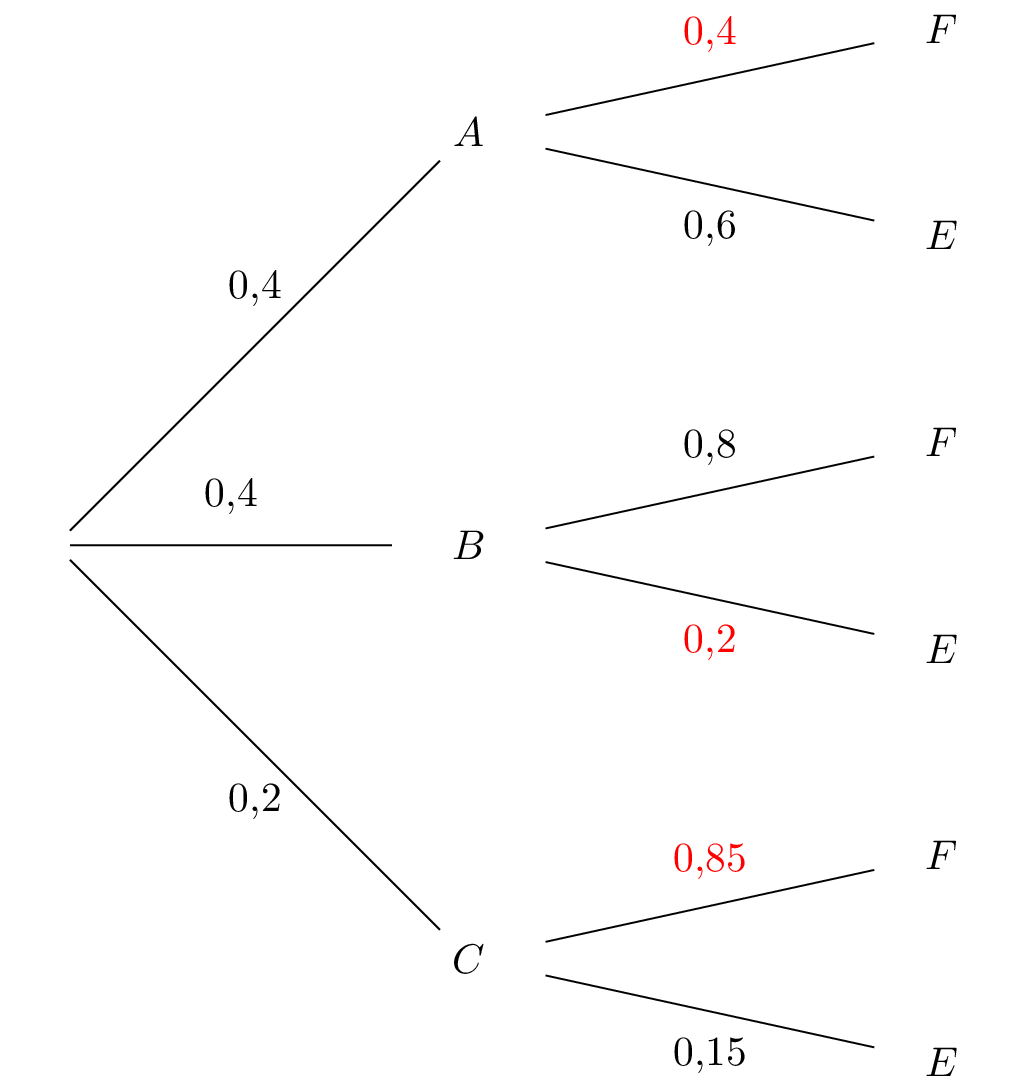
A,BA,B et CC forment une partition de l'univers.
D'après la formule des probabilités totales on a :
P(F)=P(A∩F)+P(B∩F)+P(C∩F)P\left(F\right)=P\left(A\cap F\right)+P\left(B\cap F\right)+P\left(C\cap F\right) équivaut successivement à
P(F)=P(A)×PA(F)+P(B)×PB(F)+P(C)×PC(F)P\left(F\right)=P\left(A\right)\times P_{A} \left(F\right)+P\left(B\right)\times P_{B} \left(F\right)+P\left(C\right)\times P_{C} \left(F\right)
Soit : P(F)=0,4×0,4+0,4×0,8+0,2×0,85P\left(F\right)=0,4\times 0,4+0,4\times 0,8+0,2\times 0,85
Ainsi :
P(F)=0,65P\left(F\right)=0,65
Question 4

On interroge au hasard une famille passant ses vacances en France.
Calculer la probabilité que la famille ait un enfant.

Correction
Il s'agit ici d'une forme avec un « sachant » .
On pourrait traduire la question de la manière suivante ; sachant{\color{blue}{\text{sachant}}} que la famille passe ses vacances en France quelle est la probabilité que la famille ait un enfant.
PF(A)=P(A∩F)P(F)P_{F} \left(A\right)=\frac{P\left(A\cap F\right)}{P\left(F\right)}
PF(A)=P(A)×PA(F)P(F)P_{F} \left(A\right)=\frac{P\left(A\right)\times P_{A} \left(F\right)}{P\left(F\right)}
PF(A)=0,4×0,40,65P_{F} \left(A\right)=\frac{0,4\times 0,4}{0,65}
D'où :
PF(A)=1665≈0,246P_{F} \left(A\right)=\frac{16}{65} \approx 0,246

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.