Probabilités conditionnelles - Exercice 3

8 min
15
Question 1
Soit l'arbre pondéré suivant :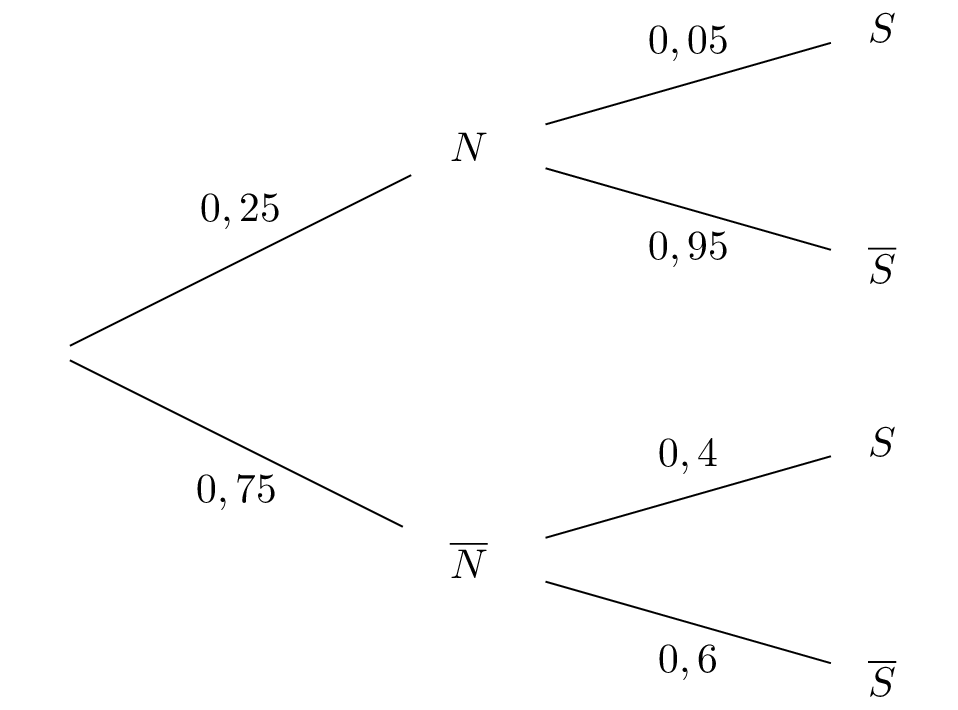

Déterminer p(S)p\left(S\right)

Correction
NN et N‾\overline{N} forment une partition de l'univers.
D'après la formule des probabilités totales on a :
P(S)=P(N∩S)+P(N‾∩S)P\left(S\right)=P\left(N\cap S\right)+P\left(\overline{N}\cap S\right)
P(S)=P(N)×PN(S)+P(N‾)×PN‾(S)P\left(S\right)=P\left(N\right)\times P_{N} \left(S\right)+P\left(\overline{N}\right)\times P_{\overline{N}} \left(S\right)
Soit : P(S)=0,25×0,05+0,75×0,4P\left(S\right)=0,25\times 0,05 +0,75\times 0,4
Ainsi :
P(S)=0,3125P\left(S\right)=0,3125

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.