Probabilités conditionnelles et loi binomiale
Loi binomiale - Exercice 3
25 min
35
Dans une fête foraine, un organisateur de jeux dispose de urnes comportant chacune boules.
L'urne comporte boules vertes, boule rouge et boules bleues.
L'urne comporte boules bleues et boules rouges.
Le déroulement du jeu est le suivant :
Le joueur tire une boule de l'urne :
L'urne comporte boules vertes, boule rouge et boules bleues.
L'urne comporte boules bleues et boules rouges.
Le déroulement du jeu est le suivant :
Le joueur tire une boule de l'urne :
- S'il tombe sur une boule verte le jeu s'arrête.
- S'il tombe sur une boule rouge ou bleue, il tire une boule de l'urne .
- V1 l'événement : "la boule est verte lors du premier tirage dans l'urne".
- R1 l'événement : "la boule est rouge lors du premier tirage dans l'urne".
- B1 l'événement : "la boule est bleue lors du premier tirage dans l'urne".
- R2 l'événement : "la boule est rouge lors du deuxième tirage dans l'urne".
- B2 l'événement : "la boule est bleue lors du deuxième tirage dans l'urne".
Question 1
Construire un arbre pondéré résumant la situation.
Correction
On remplit l'arbre pondéré par les données de l'exercice :
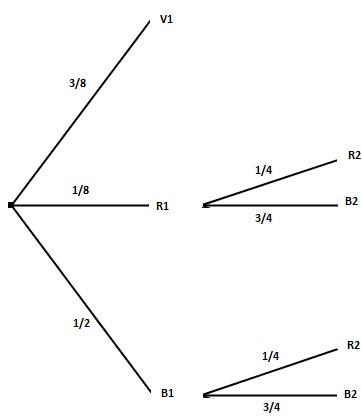

Question 2
Calculer la probabilité de l'évènement H « tirer deux boules bleues ».
Correction
et forment une partition de l'univers.
D'après la formule des probabilités totales on a :
Calculons :
d'où :
On a une chance sur de tirer deux boules bleues.
D'après la formule des probabilités totales on a :
Calculons :
d'où :
On a une chance sur de tirer deux boules bleues.
Question 3
Calculer la probabilité de l'évènement J « tirer une boule rouge »
Correction
Pour avoir une boule rouge, il y a deux possibilités :
Soit en er on tire une rouge puis ensuite une bleue
Soit en er on tire une bleue puis ensuite une rouge.
Ainsi :
équivaut successivement à :
.
On a une chance sur de tirer une boule rouge.
Si les deux boules sont rouges, le joueur gagne €, si une boule est rouge, il gagne €, sinon il ne gagne rien.
Le joueur mise €.
Soit la variable aléatoire représentant le gain du joueur.
Soit en er on tire une rouge puis ensuite une bleue
Soit en er on tire une bleue puis ensuite une rouge.
Ainsi :
équivaut successivement à :
.
On a une chance sur de tirer une boule rouge.
Si les deux boules sont rouges, le joueur gagne €, si une boule est rouge, il gagne €, sinon il ne gagne rien.
Le joueur mise €.
Soit la variable aléatoire représentant le gain du joueur.
Question 4
Déterminer la loi de probabilité de
Correction
Notons l'évènement deux boules sont rouges et l'évènement une boule est rouge.
Nous avons déjà calculé à la question 3.
Calculons :
équivaut successivement à :
Le gain du joueur est la somme reçue moins sa mise.
Ainsi, prendra les valeurs .
On va traduire ces informations dans un tableau que l'on appellera loi de probabilité :
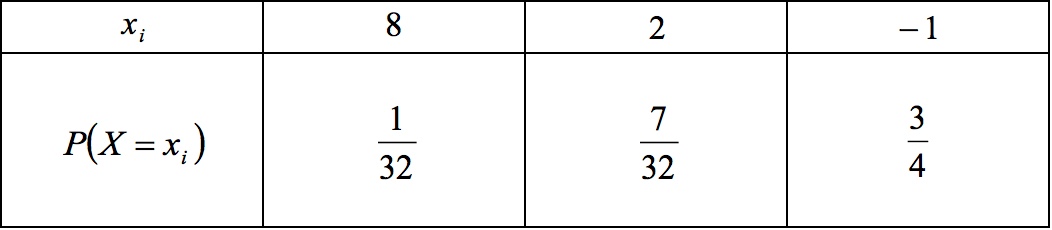
Pour obtenir , on sait que :
Soit :
Ainsi :
Nous avons déjà calculé à la question 3.
Calculons :
équivaut successivement à :
Le gain du joueur est la somme reçue moins sa mise.
Ainsi, prendra les valeurs .
On va traduire ces informations dans un tableau que l'on appellera loi de probabilité :

Pour obtenir , on sait que :
Soit :
Ainsi :
Question 5
Calculer l'espérance mathématiques de et en donner une interprétation.
Correction
On appelle l'espérance mathématique de la variable , la valeur définie par :
Autrement dit :
Il en résulte que : Autrement dit :
Soit : c'est-à-dire :
En moyenne le joueur perdra € par partie en jouant un très grand nombre de fois.