Exercices types : $$1$$^ère partie - Exercice 2

Avec les données du texte, on peut dresser l'arbre pondéré traduisant l'énoncé.
Il vient alors que :

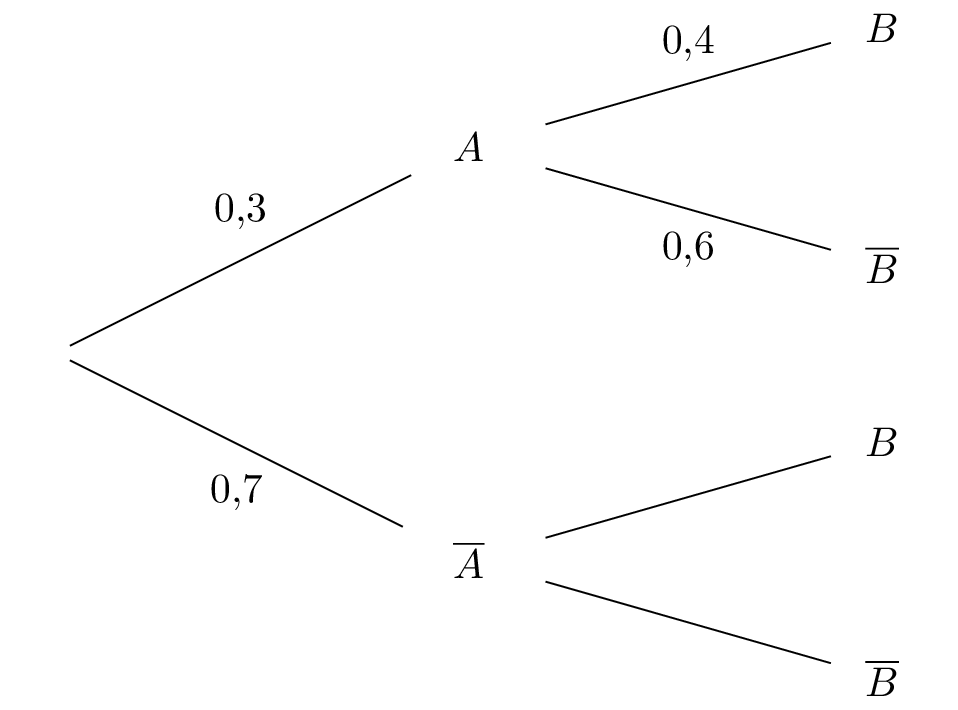
Nous devons calculer :
$$P\left(A\cap \overline{B}\right)=P\left(A\right)\times P_{A} \left(\overline{B}\right)$$
$$P\left(A\cap \overline{B}\right)=0,3\times 0,6$$
Ainsi :

Nous devons calculer $$P\left(\overline{A}\cap \overline{B}\right)$$ .
Or, nous ne pouvons pas directement calculer cette valeur.
Autrement dit $$P\left(\overline{B}\right)=0,32$$
Les évènements $$A$$ et $$\overline{A}$$ forment une partition de l'univers.
D'après la formule des probabilités totales, on a :
$$p\left(\overline{B}\right)=P\left(A\cap \overline{B}\right)+P\left(\overline{A}\cap \overline{B}\right)$$ équivaut successivement à :
$$0,32=0,18+P\left(\overline{A}\cap \overline{B}\right)$$
$$P\left(\overline{A}\cap \overline{B}\right)=0,32-0,18$$
Ainsi :

On cherche cette fois à calculer une probabilité conditionnelle. On pourrait traduire la question de la manière suivante : $${\color{blue}{\text{sachant}}}$$ que le client consomme des produits étrangers, quelle est la probabilité qu'il ne consomme pas de produit BIO.
Nous devons calculons : $$P_{\overline{B}} \left(\overline{A}\right)=\frac{P\left(\overline{A}\cap \overline{B}\right)}{P\left(\overline{B}\right)}$$
Ainsi : $$P_{\overline{B}} \left(\overline{A}\right)=\frac{0,14}{0,32}$$
D'où :

On doit calculer : $$P\left(X=2\right)$$
$$\red{\text{Avec une Texas :}}$$ pour $$P\left(X=2\right)$$ on tape :
2^nd - DISTR -- puis choisir
BinomFdp(valeur de n, valeur de p, valeur de k) c'est-à-dire ici BinomFdp($$2$$, $$0,68$$ , $$0$$) puis on tape sur enter et on obtient :
arrondi à $$10^{-2}$$ près.
Pour certaine version de Texas, on aura BinomPdf au lieu de BinomFdp.

$$\red{\text{Avec une calculatrice Casio Graph 35+ ou modèle supérieur :}}$$ pour $$P\left(X=2\right)$$ on tape :
Choisir Menu Stat puis DIST puis BINM et prendre BPD puis VAR.
On remplit le tableau de la manière qui suit :

puis on tape sur EXE et on obtient :
arrondi à $$10^{-2}$$ près.