Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Tchat avec un prof
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercice 5 - Exercice 1
1 min
0
L’exploitant d’une forêt communale décide d’abattre des arbres afin de les vendre, soit aux habitants, soit à des entreprises. On admet que :
parmi les arbres abattus, sont des chênes, sont des sapins et les autres sont des arbres d’essence secondaire (ce qui signifie qu’ils sont de moindre valeur) ; des chênes et des sapins abattus sont vendus aux habitants de la commune ; les trois quarts des arbres d’essence secondaire abattus sont vendus à des entreprises.
Question 1
Partie A
Parmi les arbres abattus, on en choisit un au hasard. On considère les évènements suivants :
: « l’arbreabattu est un chêne » ; : « l’arbre abattu est un sapin » ; : « l’arbre abattu est un arbre d’essence secondaire » ; : « l’arbre abattu est vendu à un habitant de la commune » .
Parmi les arbres abattus, on en choisit un au hasard. On considère les évènements suivants :
ANT>ILLES GUYANNE 2019 JUIN Construire un arbre pondéré complet traduisant la situation.
Correction
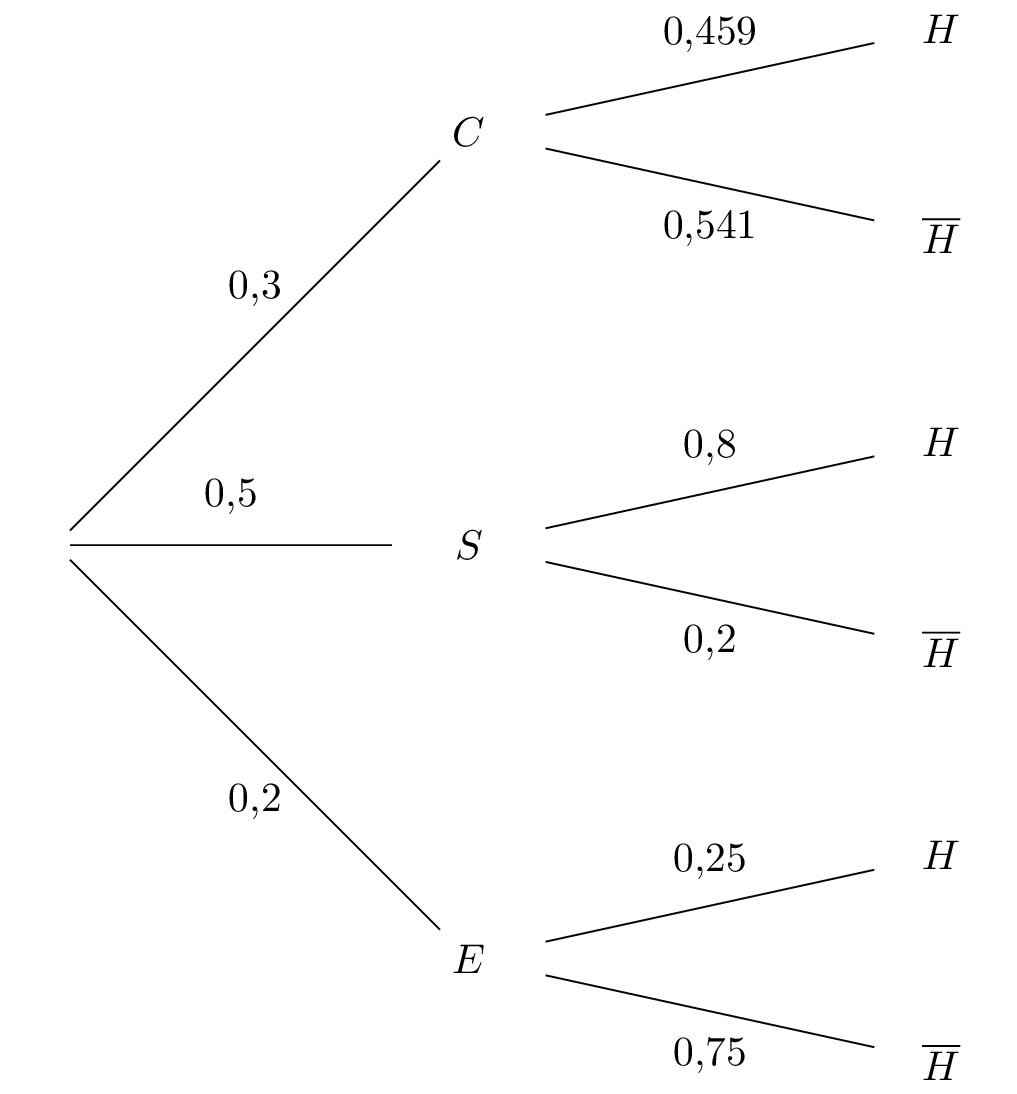
Question 2
Calculer la probabilité que l’arbre abattu soit un chêne vendu à un habitant de la commune.
Correction

D'où :
La probabilité que l’arbre abattu soit un chêne vendu à un habitant de la commune est .
Question 3
Justifier que la probabilité que l’arbre abattu soit vendu à un habitant de la commune est égale à .
Correction

D'après la formule des probabilités totales, on a :
équivaut successivement à :
Question 4
Quelle est la probabilité qu’un arbre abattu vendu à un habitant de la commune soit un sapin? On donnera le résultat arrondi à .
Correction

On pourrait traduire la question de la manière suivante ; que l'arbre abattu a été vendu à un habitant de la commune, quelle est la probabilité que ce soit un sapin.
d'où :
Question 5
Partie B
Le nombre d’arbres sur un hectare de cette forêt peut être modélisé par une variable aléatoire suivant une loi normale d’espérance et d’écart-type .
Le nombre d’arbres sur un hectare de cette forêt peut être modélisé par une variable aléatoire suivant une loi normale d’espérance et d’écart-type .
Déterminer la probabilité qu’il y ait entre et arbres sur un hectare donné de cette forêt. On donnera le résultat arrondi à .
Correction
Pour le calcul de
Avec une calculatrice Texas, pour on tape NormalFrep(valeur min, valeur max, espérance, écart type)
C'est-à-dire ici NormalFrep( , , , ) puis on tape sur Enter et on obtient :
Avec une calculatrice Casio Graph 35+, pour on tape :
puis on tape sur EXE et on obtient :
Avec une calculatrice Texas, pour on tape NormalFrep(valeur min, valeur max, espérance, écart type)
C'est-à-dire ici NormalFrep( , , , ) puis on tape sur Enter et on obtient :
Avec une calculatrice Casio Graph 35+, pour on tape :
Normal C.D
Lower : Valeur Minimale
Upper : Valeur Maximale
: Ecart type
: Espérance
Lower : Valeur Minimale
Upper : Valeur Maximale
: Ecart type
: Espérance
puis on tape sur EXE et on obtient :
Question 6
Calculer la probabilité qu’il y ait plus de arbres sur un hectare donné de cette forêt. On donnera le résultat arrondi à .
Correction
Pour le calcul de
Avec une calculatrice Texas, pour on tape NormalFrep(valeur min, valeur max, espérance, écart type)
C'est-à-dire ici NormalFrep( , , , ) puis on tape sur Enter et on obtient :
Avec une calculatrice Casio Graph 35+, pour on tape :
puis on tape sur EXE et on obtient :
Avec une calculatrice Texas, pour on tape NormalFrep(valeur min, valeur max, espérance, écart type)
C'est-à-dire ici NormalFrep( , , , ) puis on tape sur Enter et on obtient :
Avec une calculatrice Casio Graph 35+, pour on tape :
Normal C.D
Lower : Valeur Minimale
Upper : Valeur Maximale
: Ecart type
: Espérance
Lower : Valeur Minimale
Upper : Valeur Maximale
: Ecart type
: Espérance
puis on tape sur EXE et on obtient :
Question 7
Partie C
L’exploitant affirme que la densité de sapins dans cette forêt communale est de sapin pour arbres.
L’exploitant affirme que la densité de sapins dans cette forêt communale est de sapin pour arbres.
Sur une parcelle, on a compté sapins dans un échantillon de arbres. Ce résultat remet-il en cause l’affirmation de l’exploitant?
Correction
Il faut vérifier les conditions suivantes , et . Ici et .
Remarque : en référence à l’exploitant affirme que la densité de sapins dans cette forêt communale est de sapin pour arbres.
Les trois conditions sont réalisées, on peut donc calculer l'intervalle de fluctuation asymptotique au seuil de .
On a alors :
Ici est une valeur approchée par défaut de
Ici est une valeur approchée par excès de
Or , donc cela ne remet pas en cause l’affirmation de l’exploitant.
Remarque : en référence à l’exploitant affirme que la densité de sapins dans cette forêt communale est de sapin pour arbres.
- donc
- donc
- donc
Les trois conditions sont réalisées, on peut donc calculer l'intervalle de fluctuation asymptotique au seuil de .
On a alors :
Ici est une valeur approchée par défaut de
Ici est une valeur approchée par excès de
Or , donc cela ne remet pas en cause l’affirmation de l’exploitant.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.