Les suites numériques
Exercice 3 - Exercice 1
1 min
0
Cet exercice est un questionnaire à choix multiples.
Pour chaque question posée, une seule des réponses proposées est exacte.
On demande bien sûr de justifier.
Pour chaque question posée, une seule des réponses proposées est exacte.
On demande bien sûr de justifier.
Question 1
La somme est égale à :
-
-
-
Correction
La bonne réponse est b
Il vient alors :
car
Nous partons de qui est le premier terme à . Nous avons donc termes.
On applique la formule :
La somme des termes d'une suite géométrique est donnée par la formule suivante :
Il s'agit de la somme des termes d'une suite géométrique de raison Il vient alors :
car
Nous partons de qui est le premier terme à . Nous avons donc termes.
On applique la formule :
Question 2
On considère la suite définie par .
Alors on peut en déduire que la suite est :
- Géométrique de raison
- Géométrique de raison
- Arithmétique de raison
Alors on peut en déduire que la suite est :
- Géométrique de raison
- Géométrique de raison
- Arithmétique de raison
Correction
La bonne réponse est a.
équivaut successivement à
Il s'agit donc d'une suite géométrique de raison
équivaut successivement à
Il s'agit donc d'une suite géométrique de raison
Question 3
On considère la suite définie par .
La limite de la suite est égale à :
-
-
-
La limite de la suite est égale à :
Correction
La bonne réponse est a.
que l'on peut écrire .
- Si alors .
- Si alors .
- Comme alors :
- De plus, alors :
Question 4
On considère la suite arithmétique de premier terme et de raison .
Quel est le rôle de l'algorithme suivant ?
Variables
et sont deux entiers naturels
Initialisation
prend la valeur
prend la valeur
Traitement
Tant que
prend la valeur
prend la valeur
Fin tant que
Sortie
Afficher
- Il calcule
- Il calcule le plus petit entier tel que
- Il calcule le plus grand entier tel que
Quel est le rôle de l'algorithme suivant ?
Variables
et sont deux entiers naturels
Initialisation
prend la valeur
prend la valeur
Traitement
Tant que
prend la valeur
prend la valeur
Fin tant que
Sortie
Afficher
et sont deux entiers naturels
Initialisation
prend la valeur
prend la valeur
Traitement
Tant que
prend la valeur
prend la valeur
Fin tant que
Sortie
Afficher
- Il calcule
- Il calcule le plus petit entier tel que
- Il calcule le plus grand entier tel que
Correction
La bonne réponse est b.
D'après l'énoncé, la suite arithmétique s'écrit avec comme premier terme .
Il suffit de calculer les termes , et ainsi de suite jusqu'au moment où la valeur dépassera .
On indiquera ensuite le rang tel que .
Donc l'algorithme calcule le plus petit entier tel que .
D'après l'énoncé, la suite arithmétique s'écrit avec comme premier terme .
Il suffit de calculer les termes , et ainsi de suite jusqu'au moment où la valeur dépassera .
On indiquera ensuite le rang tel que .
Donc l'algorithme calcule le plus petit entier tel que .
Question 5
On considère l'algorithme suivant :
Variables
, et sont trois entiers naturels
Initialisation
prend la valeur
Traitement
Saisir
Pour allant de à
prend la valeur
Fin pour
Sortie
Afficher
Quelle est la valeur affichée par cet algorithme lorsqu'on choisit ?
-
-
-
Variables
, et sont trois entiers naturels
Initialisation
prend la valeur
Traitement
Saisir
Pour allant de à
prend la valeur
Fin pour
Sortie
Afficher
, et sont trois entiers naturels
Initialisation
prend la valeur
Traitement
Saisir
Pour allant de à
prend la valeur
Fin pour
Sortie
Afficher
Quelle est la valeur affichée par cet algorithme lorsqu'on choisit ?
Correction
La bonne réponse est c.
On calcule pour chaque , la valeur de associée.
On dresse le tableau suivant :
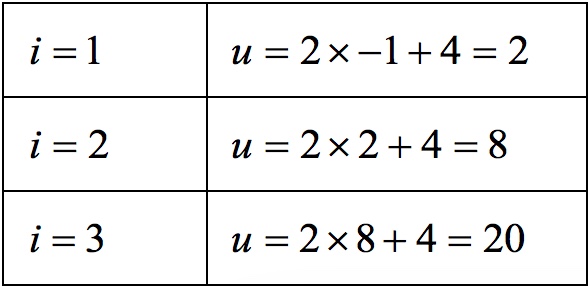
On calcule pour chaque , la valeur de associée.
On dresse le tableau suivant :
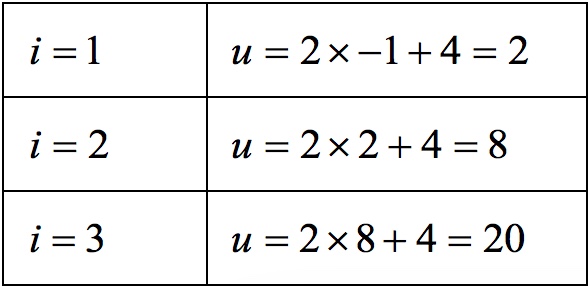
Question 6
On place euros sur un livret qui propose une augmentation de annuelle.
Chaque année les intérêts gagnés permettent également de générer des intérêts.
On appelle cela un intérêt composé.
Quelle est le montant sur le livret dans ans (arrondi à l'entier supérieur) ?
-
-
-
Chaque année les intérêts gagnés permettent également de générer des intérêts.
On appelle cela un intérêt composé.
Quelle est le montant sur le livret dans ans (arrondi à l'entier supérieur) ?
Correction
La bonne réponse est b
On note le montant sur le livret la ère année.
Chaque année, il y a une augmentation de qui correspond à un coefficient multiplicateur noté .
Cet investissement traduit une suite géométrique de raison et de premier terme .
On exprime alors en fonction de .
Ainsi .
Autrement dit .
Le montant sur le livret dans ans correspond à .
Finalement,
(arrondi à l'entier supérieur)
On note le montant sur le livret la ère année.
Chaque année, il y a une augmentation de qui correspond à un coefficient multiplicateur noté .
Cet investissement traduit une suite géométrique de raison et de premier terme .
On exprime alors en fonction de .
Ainsi .
Autrement dit .
Le montant sur le livret dans ans correspond à .
Finalement,
Question 7
Une baisse de suivi d'une hausse de équivaut à :
- Une baisse
- Une hausse
- Ni l'un, ni l'autre
- Une baisse
- Une hausse
- Ni l'un, ni l'autre
Correction
La bonne réponse est b.
Il faut multiplier les coefficients multiplicateurs.
Ainsi .
Finalement, une baisse de suivi d'une hausse de équivaut à une diminution de .
- une baisse de correspond à un coefficient multiplicateur qui vaut
- une hausse de correspond à un coefficient multiplicateur qui vaut
Il faut multiplier les coefficients multiplicateurs.
Ainsi .
Finalement, une baisse de suivi d'une hausse de équivaut à une diminution de .
Question 8
Pour compenser une hausse de , il faut appliquer une baisse de :
-
-
-
Correction
La bonne réponse est b.
Notons le taux réciproque associée à une hausse de .
Ainsi
Pour compenser une hausse de , il faut appliquer une baisse de .
Soit un taux d'évolution.
On note le taux réciproque associée à .
Alors .
Cela signifie que l'évolution réciproque revient à trouver le taux d'évolution qu'il faudrait appliquer pour retrouver sa valeur initiale.
Une hausse de correspond à un coefficient multiplicateur qui vaut .On note le taux réciproque associée à .
Alors .
Cela signifie que l'évolution réciproque revient à trouver le taux d'évolution qu'il faudrait appliquer pour retrouver sa valeur initiale.
Notons le taux réciproque associée à une hausse de .
Ainsi
Pour compenser une hausse de , il faut appliquer une baisse de .
Question 9
On considère la suite arithmétique de premier terme et de raison . La somme est égale à :
-
-
-
Correction
La bonne réponse est b.
On exprime alors en fonction de .
Ainsi .
Autrement dit .
On calcule maintenant
On applique la formule :
.
On a termes en tout car on part de et on va jusqu'à .
La somme des termes d'une suite arithmétique est donnée par la formule suivante :
On sait qu'il s'agit d'une suite arithmétique de premier terme et de raison .On exprime alors en fonction de .
Ainsi .
Autrement dit .
On calcule maintenant
On applique la formule :
.
On a termes en tout car on part de et on va jusqu'à .
Pour savoir le nombre de termes présents dans une somme, faites le calcul suivant :
La somme comprend termes. Ici le plus grand indice est , le plus petit indice est . Ainsi le nombre de termes est égale à : . Nous avons donc termes. La somme comprend termes. Ici le plus grand indice est , le plus petit indice est . Ainsi le nombre de termes est égale à : . Nous avons donc termes. La somme comprend termes. Ici le plus grand indice est , le plus petit indice est . Ainsi le nombre de termes est égale à : . Nous avons donc termes. La somme comprend termes. Ici le plus grand indice est , le plus petit indice est . Ainsi le nombre de termes est égale à : . Nous avons donc termes.
Question 10
Soit un entier naturel.
On considère la suite définie par : .
On définit également la suite définie par .
On considère la suite définie par : .
On définit également la suite définie par .
Alors la suite est :
- Arithmétique de raison
- Géométrique de raison
- Géométrique de raison
- Arithmétique de raison
- Géométrique de raison
- Géométrique de raison
Correction
La bonne réponse est c.
On a donc
Or
On va écrire maintenant l'expression au rang , il vient alors que :
On connait l'expression de , on la remplace et on obtient :
.
Or donc
Ainsi la suite est géométrique de raison .
On a donc
Or
On va écrire maintenant l'expression au rang , il vient alors que :
On connait l'expression de , on la remplace et on obtient :
.
Or donc
Ainsi la suite est géométrique de raison .
Question 11
On considère l'algorithme ci-dessous :
Pour allant de à
Fin Pour
Pour allant de à
Fin Pour
On affecte à la variable . Que contient la variable , arrondie au dixième, à la fin de l’exécution de l’algorithme? -
-
-
Correction
La bonne réponse est a.
Nous appliquons l'algorithme, il vient alors que :

Nous appliquons l'algorithme, il vient alors que :
