La fonction logarithme
Exercices types : applications à l'économie - Exercice 2
20 min
40
Soit la fonction définie sur l’intervalle par : .
Question 1
Une entreprise fabrique des objets. Le coût unitaire (en euros) pour centaines d’objets produits est égal à .
Montrer que, pour tout , on a : .
Correction
est dérivable sur . On a :
Question 2
Étudier les variations de sur l’intervalle .
Correction
Nous savons que .
Comme on travaille sur l'intervalle alors le dénominateur est strictement positif.
Il en résulte que le signe de dépend du numérateur .
est une équation du second degré, pour étudier son signe on va utiliser le discriminant .
On donnera directement les résultats : ; et .
Comme , la parabole est tournée vers le haut c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
On en déduit le tableau de variation de .
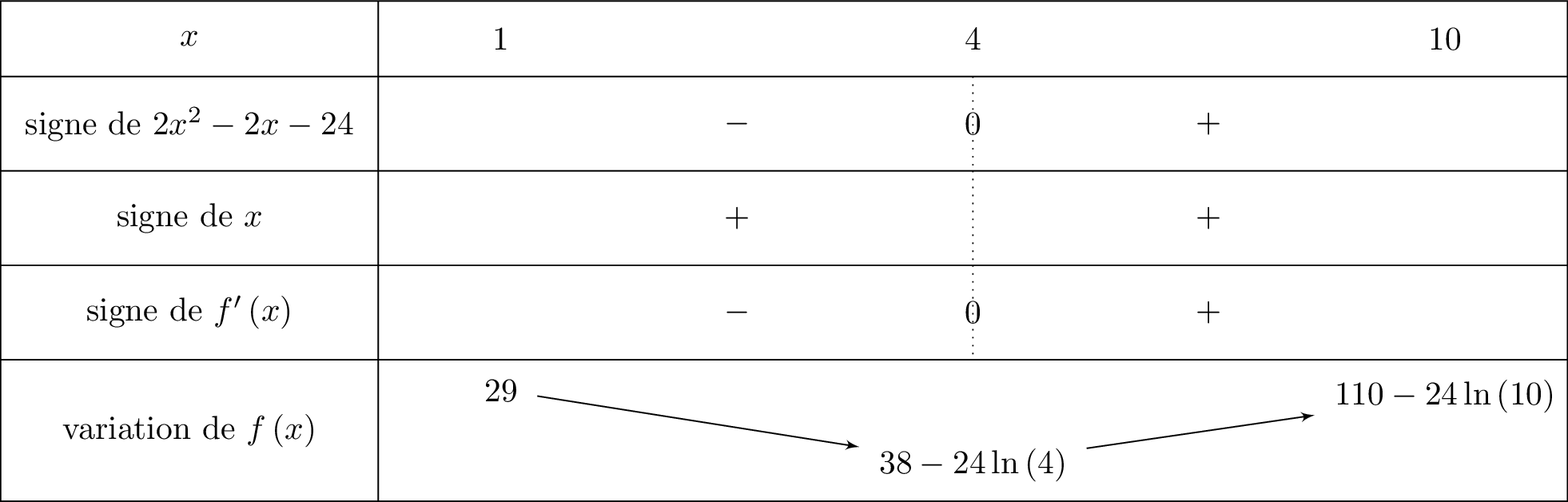
d'où : d'où : d'où :
Comme on travaille sur l'intervalle alors le dénominateur est strictement positif.
Il en résulte que le signe de dépend du numérateur .
est une équation du second degré, pour étudier son signe on va utiliser le discriminant .
On donnera directement les résultats : ; et .
Comme , la parabole est tournée vers le haut c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
On en déduit le tableau de variation de .

Question 3
Pour combien d’objets produits, le coût de fabrication par objet est-il minimum? Donner la valeur arrondie au centime d’euros de ce coût minimum.
Correction

Le coût de fabrication par objet est minimal pour objets. Il est alors d’environ euros par objet.