La fonction logarithme
Exercices types : ème partie - Exercice 4
25 min
40
Question 1
On considère la fonction définie sur l'intervalle par .
On note la dérivée de . Calculer .
Correction
est dérivable sur .
On reconnaît la forme : avec et .
Ainsi et .
Il vient alors que :
équivaut successivement à :
On reconnaît la forme : avec et .
Ainsi et .
Il vient alors que :
équivaut successivement à :
Question 2
Donner la valeur exacte de .
Correction
Ainsi :
Question 3
Etudier les variations de .
Correction
Il nous faut maintenant étudier le signe de .
Or, nous savons que :
Pour tout , on vérifie aisément que . Le signe de dépend alors de .
Le tableau de variation de est donnée ci-dessous :
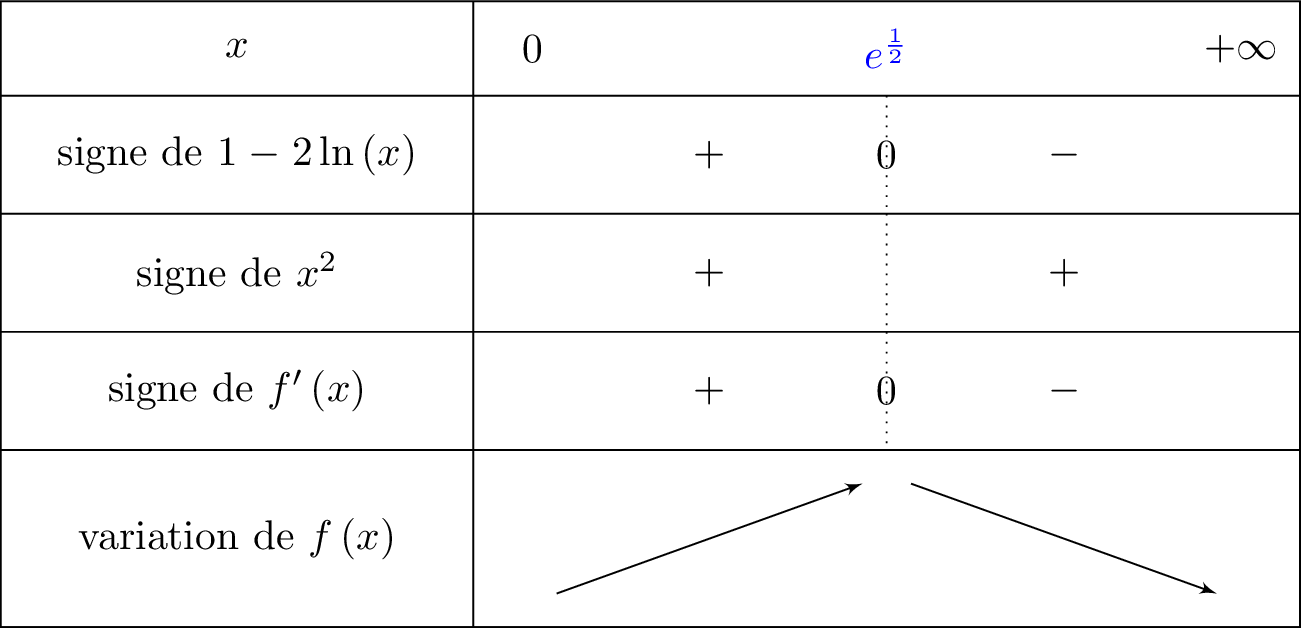
Or, nous savons que :
Pour tout , on vérifie aisément que . Le signe de dépend alors de .
Le tableau de variation de est donnée ci-dessous :

Question 4
Montrer que pout tout réel strictement positif, on a : .
Correction
est dérivable sur .
On reconnaît la forme : avec et .
Ainsi et .
Il vient alors que :
Ainsi :
On reconnaît la forme : avec et .
Ainsi et .
Il vient alors que :
Ainsi :
Question 5
Justifier que la courbe admet un point d'inflexion dont on précisera les coordonnées.
Correction
- possède un point d'inflexion lorsque sa dérivée seconde s'annule et change de signe en ce point.
Pour tout réel strictement positif, on a alors :
équivaut successivement à :
. Nous avons maintenant l'abscisse du point d'inflexion. Pour calculer son ordonnée, il nous reste à calculer .
Finalement, les coordonnées du point d'inflexion sont alors .
Question 6
Etudier la convexité de .
Correction
Pour étudier la convexité de la fonction , il faut étudier le signe de .
Pour tout , on vérifie aisément que .
Le signe de dépend alors de .
Il vient alors que :
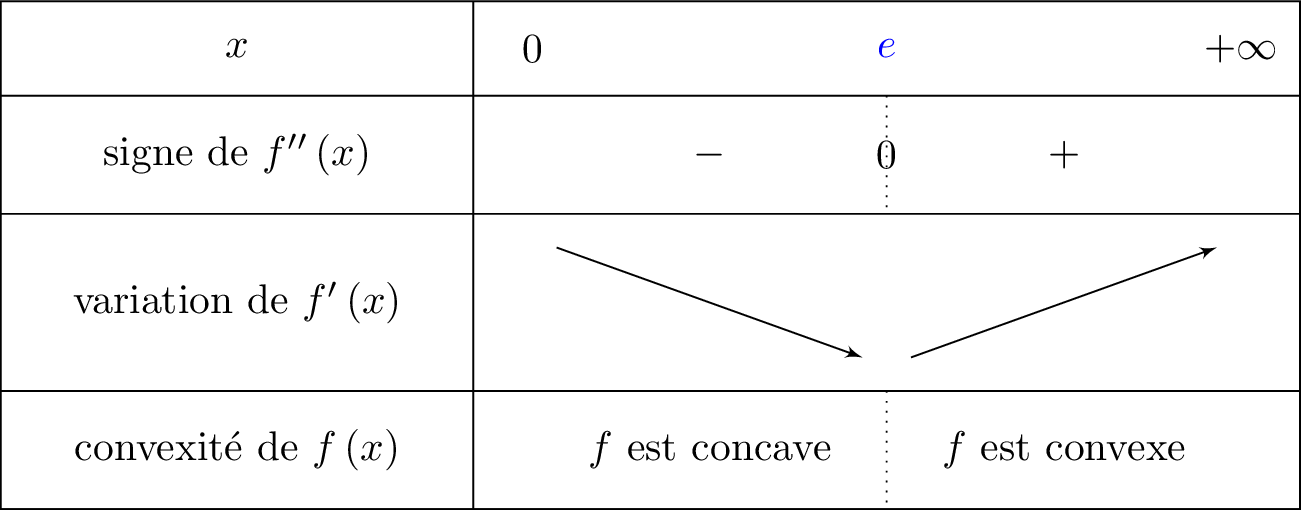
- Lorsque sur un intervalle alors est convexe.
- Lorsque sur un intervalle alors est concave.
Le signe de dépend alors de .
Il vient alors que :
