La fonction logarithme

Exercices types : 22ème partie - Exercice 3

12 min
20
Soit la fonction ff définie sur ]0;+∞[\left]0;+\infty \right[ par : f(x)=ln⁡(x)+1f\left(x\right)=\ln \left(x\right)+1. On note CfC_{f} la courbe représentative de la fonction ff.
On note f′f' la fonction dérivée de la fonction ff sur ]0;+∞[\left]0;+\infty \right[.
Question 1
Pour chacune des quatre affirmations suivantes, indiquer si elle est vraie ou fausse en justifiant la réponse.

Affirmation 1 : La fonction ff est décroissante sur ]0;+∞[\left]0;+\infty \right[.

Correction
L’affirmation 1 est Fausse.\red{\text{L'affirmation 1 est Fausse.}}
ff est dérivable sur ]0;+∞[\left]0;+\infty \right[.
Ainsi :
f′(x)=1xf'\left(x\right)=\frac{1}{x}.
Or, pour tout réel xx appartenant à l'intervalle ]0;+∞[\left]0;+\infty \right[, on vérifie facilement que f′(x)>0f'\left(x\right)>0.
La fonction ff est donc strictement croissante sur ]0;+∞[\left]0;+\infty \right[.
Question 2

Affirmation 2 : L'équation f(x)=2f\left(x\right)=2 possède une unique solution sur l'intervalle [1;10]\left[1;10 \right].

Correction
L’affirmation 2 est Vraie.\red{\text{L'affirmation 2 est Vraie.}}
Nous savons d'après la question précédente que la fonction ff strictement croissante sur ]0;+∞[\left]0;+\infty \right[.
De plus :
f(1)=ln⁡(1)+1f\left(1\right)=\ln \left(1\right)+1 d'où : f(1)=1f\left(1\right)=1
f(10)=ln⁡(10)+1f\left(10\right)=\ln \left(10\right)+1 d'où : f(10)≈3,30f\left(10\right)\approx3,30
Il vient alors que :
Nous faisons apparaître la valeur 22 recherché dans le tableau de variation donnée. Il vient alors que :
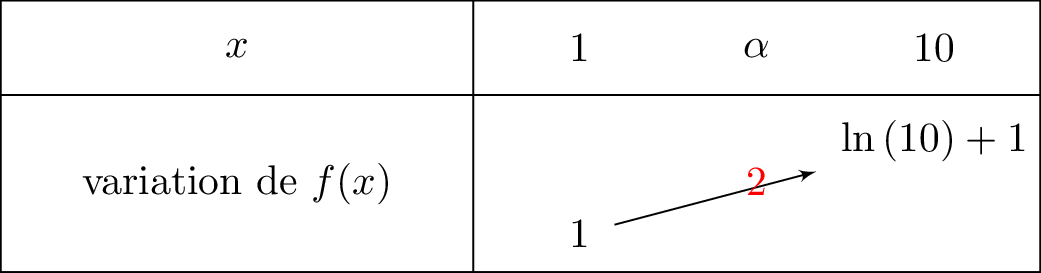
Sur [1;10]\left[1;10\right], la fonction ff est continue et strictement croissante.
De plus, f(1)=1f\left(1\right)=1 et f(10)=ln⁡(10)+1f\left(10\right)=\ln \left(10\right)+1 .
Or 0∈[1;ln⁡(10)+1]0\in \left[1;\ln \left(10\right)+1\right], donc d'après le théorème des valeurs intermédiaires, il existe une unique solution α\alpha appartenant à l'intervalle [1;10]\left[1;10\right] tel que f(x)=2f\left(x\right)=2.
Question 3

Affirmation 3 : Il existe au moins un point de la courbe CfC_{f} pour lequel la tangente en ce point est située entièrement sous la courbe CfC_{f}.

Correction
L’affirmation 3 est Fausse.\red{\text{L'affirmation 3 est Fausse.}}
Pour étudier la convexité de la fonction ff, il faut étudier le signe de f′′f''.
  • Lorsque f′′(x)≥0f''\left(x\right)\ge 0 sur un intervalle [a,b]\left[a,b\right] alors ff est convexe et la courbe CfC_{f} est toujours située au-dessus des tangentes en tous les points de l'intervalle [a,b]\left[a,b\right]
  • Lorsque f′′(x)≤0f''\left(x\right)\le 0 sur un intervalle [a,b]\left[a,b\right] alors ff est concave et la courbe CfC_{f} est toujours située en dessous des tangentes en tous les points de l'intervalle [a,b]\left[a,b\right].
ff est dérivable sur ]0;+∞[\left]0;+\infty \right[.
Ainsi :
f′(x)=1xf'\left(x\right)=\frac{1}{x} et f′′(x)=−1x2f''\left(x\right)=-\frac{1}{x^{2}}.
Or, pour tout réel xx appartenant à ]0;+∞[\left]0;+\infty \right[, on vérifie facilement que f′′(x)<0f''\left(x\right)<0. La fonction ff est donc concave.
Question 4

Affirmation 4 : On note FF la primitive sur ]0;+∞[\left]0;+\infty \right[ de la fonction ff qui vérifie F(1)=0F\left(1\right)=0. Pour tout réel xx strictement positif, F(x)=xln⁡(x)F\left(x\right)=x\ln \left(x\right).

Correction
L’affirmation 4 est Vraie.\red{\text{L'affirmation 4 est Vraie.}}
D'une part : F(1)=1×ln⁡(1)F\left(1\right)=1\times\ln \left(1\right) c'est à dire : F(1)=0F\left(1\right)=0.
Dans le cas où une primitive FF est donnée, il vous suffit de dériver FF et d'obtenir comme résultat ff.
Autrement dit, il faut que : F′(x)=f(x)F'\left(x\right)=f\left(x\right)
Maintenant calculons la dérivée de FF.
Ici on reconnaît la forme : (uv)′=u′v+uv′\left(uv\right)'=u'v+uv' avec u(x)=xu\left(x\right)=x et v(x)=ln⁡(x)v\left(x\right)=\ln \left(x\right).
Ainsi : u′(x)=1u'\left(x\right)=1 et v′(x)=1xv'\left(x\right)=\frac{1}{x} .
Il vient alors que :
F′(x)=1×ln⁡(x)+x×1xF'\left(x\right)=1\times \ln \left(x\right)+x\times \frac{1}{x} équivaut successivement à :
F′(x)=ln⁡(x)+xxF'\left(x\right)=\ln \left(x\right)+\frac{x}{x}
D'où :
F′(x)=ln⁡(x)+1=f(x)F'\left(x\right)=\ln \left(x\right)+1=f\left(x\right)
Question 5

Affirmation 5 : Soit ff la fonction définie sur ]0;+∞[\left]0;+\infty \right[ par f(x)=11+5ln⁡(x)f\left(x\right)=11+5\ln \left(x\right). L'équation f(x)=0f\left(x\right)=0 a comme solution x=e−115x=e^{\frac{-11}{5} }

Correction
L’affirmation 5 est Vraie.\red{\text{L'affirmation 5 est Vraie.}}
11+5ln⁡(x)=011+5\ln \left(x\right)=0 équivaut successivement à :
5ln⁡(x)=−115\ln \left(x\right)=-11
ln⁡(x)=−115\ln \left(x\right)=\frac{-11}{5}
ln⁡(x)=ln⁡(e−115)\ln \left(x\right)=\ln \left(e^{\frac{-11}{5}} \right) car ln⁡(ea)=a\ln \left(e^{a} \right)=a
Ainsi :
x=e−115x=e^{\frac{-11}{5}}